Influence of S-Curves on Use of Inventive Principles

Darrell Mann
Industrial Fellow, Department of Mechanical Engineering
University of Bath
Bath, BA2 7AY, UK
Phone: +44 (1225) 826465
Fax: +44 (1225) 826928
E-mail: D.L.Mann@bath.ac.uk

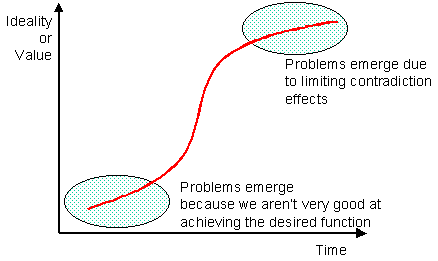
This article discusses emerging correlations between evolutionary S-curves and the 40 Inventive Principles contained within TRIZ. The position of a system - be it technical or non-technical - on its current S-curve plays a significant role in determining which TRIZ tools may be deployed to improve the system. We may see, for example, that our approaches when the system are markedly different at the two extreme ends of the curve - Figure 1.

Figure 1: Position on S-Curve Influences Problem Solution Strategy

Given the two ends of the S-curve, it is commonly observed that the Substance-Field Analysis method is more effective at the bottom of the curve, and that the Contradictions toolkit is most effective at the top of the curve. That being said, it is also clear that contradictions exist throughout the life of the S-curve - indeed, as long as the system exists, it will contain contradictions.

The Contradiction Matrix is of course a commonly applied means of managing the choice of when to use which of the 40 Inventive Principles. Unfortunately, for a good number of engineering problems - particularly electrical-based systems - and for just about all non-technical problems, the Matrix is not a reliable tool. A common response in these situations where the Matrix does not help, is to ask problem solvers to examine each of the 40 Principles. The main problem with this advice is that it tends to dilute the consideration of each Principle to unacceptably low levels.

While research continues to examine updates to the Matrix, there are a number of simple strategies which enable problem solvers to reduce the number of Principles which are likely to be relevant to a given situation. This article discusses one such method.

S-Curves and Trimming Trend

A previous article has discussed the correlation between an S-curve and the Trimming evolution trend (Reference 1). Figure 2 reproduces the main correlation suggested in that article.

Figure 2: Approximate Relationship Between S-Curve and System Part Count

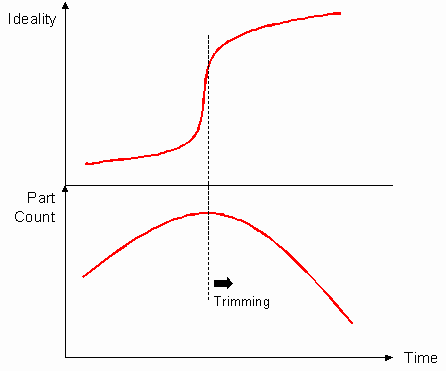
The main message from the graph is that during the initial stages of the S-curve, part count (NB phrase is intended to apply to both technical and non-technical systems again) may have to rise; and during the latter stages, the part count will become reduced.

With this increasing-then-decreasing part count idea in mind, examination of the Inventive Principles suggests that certain of the 40 involve inventive directions which also correlate to either increasing or decreasing part count:

Principles Associated With Increasing Part Count
(In numerical order)

• Principle 1 - Segmentation - usually implies increased number of components (although, for non-technical systems may well mean a re-distribution or re-organisation of existing resources rather than necessarily addition of new resources)
• Principle 7 - Nested Doll
• Principle 8 - Counterweight - implies addition of something to counter the downward tendency of the problem aspect.
• Principle 9 - Preliminary Anti-Action - as 10 below
• Principle 10 - Preliminary Action - implies supply of additional things to perform the preliminary action
• Principle 11 - Beforehand Cushioning - addition of something to counter non-desirable affect in current system.
• Principle 15 - Dynamics - transition from immobile to mobile system implies addition of components to permit relative movement of different sub-components
• Principle 23 - Feedback - addition of components required to first sense and then relay feedback messages
• Principle 24 - Intermediary
• Principle 27 - Cheap Short-Living Objects (‘replace an expensive object with a multiple of inexpensive objects, compromising certain qualities’)
• Principle 38 - Strong Oxidants (‘Enriched Atmosphere’) - addition of active elements plus possible need for additional elements to contain or control the active element.
• Principle 39 - Inert Atmosphere - similar to Principle 38; addition of inert elements may also prompt addition of other elements to contain or control the inert elements.

Principles Associated With Decreasing Part Count
(In numerical order)

• Principle 2 - Taking Out
• Principle 3 - Local Quality - implies making existing components be modified to achieve the functions of several - particularly evident as a part-count reducer in casting operations especially since casting technology has evolved to permit casting of highly complex shapes.
• Principle 5 - Merging
• Principle 6 - Universality (‘make an object or structure perform multiple functions’)
• Principle 20 - Continuity of Useful Action (‘B: eliminate all idle or intermittent actions or work’)
• Principle 25 - Self-Service
• Principle 40 - Composite Materials - combining multiple structures/functions into a coherent composite structure.

Bringing the ‘increasing’ and ‘decreasing’ Principles together onto one picture gives the reference image shown in Figure 3. It is hoped that this picture will be of some value to problem owners working in areas - particularly non-technical - where the Contradiction Matrix is not effective.

Note that some of the Principles cannot be categorised into either ‘increasing’ or ‘decreasing’ part count usage because they are either part-count neutral (‘Colour Changes’) or may cause part count to change in either direction depending on the particular circumstances of the system.

Care should be applied when employing the recommendations contained in this article in cases where systems and sub-systems are shifting to new S-curves. More will be written about the importance of S-curves and S-curve families in a future article.

1. Mann, D.L., ‘Trimming Evolution Patterns For Complex Systems’, TRIZ Journal, February 2000.