Integrated Conceptual Design With TRIZ

	Related Tools & Articles Selecting the Best Direction to Create the Ideal Product Design The QFD, TRIZ and Taguchi Connection: Customer-Driven Robust Innovation 40 Management Principles In Frequency Order
	Discussion Forum "Forbes article tells of a U.S. government-sponsored group that's going to decide in the next 2 years. Apparently in the first meeting all of the members had different ideas about how to measure innovation..." Contribute to this Discussion

By Kai Ming Yu, C.T. Lau, K.L. Tong and W.K. Wong

Abstract

In new product development, idea generation that is innovative, able to be manufactured and profitable is important. For discrete consumer products or technical systems, creative idea generation techniques advocated by psychologists, and practiced by management consultants, are usually too general for engineers. A successful product needs to implement most (if not all) functions specified in the client statement and a multitude of factors identified from consumer and competitor analyses.

Optimization techniques, however, will suit more for detailed design. QFD (quality function deployment) may link up various product development stages with the voice of the customer (VOC), but alternatives are ranked by simple weights. This paper proposes an integrated approach for inventive idea generation and multi-criteria decision-making during conceptual design. The Theory of Inventive Problem Solving (TRIZ) is employed for generating idea systematically for technical problems, while superiority and inferiority ranking (SIR) will be used for more comprehensive alternative selection. Details on how the methods complement each other to achieve innovative product development will be explained, along with an illustrative practical example.

Keywords

TRIZ, SIR, new product development, conceptual design

Introduction

New product development (NPD) is important to the growth of every company because it can contribute toward creating improved products and services, which give competitive edge to the company.²¹ In new product development, generation of ideas that are innovative, able to be manufactured and profitable is important. Design with consideration of downstream activities has been well accepted since 1982.²³ Quality function deployment attempts to link up various NPD stages with the voice of customer.¹ For discrete consumer products or technical systems, creative idea generation techniques advocated by psychologists and practiced by management consultants are usually too general for engineers.

For instance, there is the five-step model of the creative process: preparation, incubation, intimation, illumination and verification.³⁴ Edward De Bono developed lateral thinking to provoke creativity.¹⁵ A successful product needs to include most (if not all) functions specified in the client statement and a multitude of factors identified from consumer and competitor analyses. Design optimization, however, using cost function minimization cannot be done in the conceptual design stage; alternatives in QFD are ranked by simple weights. Tools are needed that can provide truly innovative ideas rather than simply creative or inventive ones.

Background

Engineering design includes conceptual, embodiment and detailed design stages.²⁷ A typical product development workflow is shown in Figure 1. As the famous inventor C. F. Kettering once said, "A problem well-stated is a problem half-solved," the conceptual design stage is further broken down into more steps (Figure 2). The integration of concept clarification, generation and selection ensures efforts and budgets are properly spent in NPD activities.

Figure 1: Typical Product Development Workflow

Figure 2: Elaborated  Conceptual Design

Theory of Inventive Problem Solving (TRIZ)

TRIZ was developed by Genrich Altshuller and his colleagues in the former U.S.S.R. starting in 1946, and is now practiced throughout the world.^3,4,5

TRIZ research is based on the hypothesis that there are universal principles of invention for creative innovations driven by advanced technology. If these principles can be identified and codified, it makes the process of invention more predictable. More than two million patents have been examined, classified by level of inventiveness and analyzed to look for the principles of innovation. The three primary findings of this research are:

1. Problems and solutions were repeated across industries and sciences,
2. Patterns of technical evolution were repeated across industries and sciences and
3. Innovations used scientific effects outside the fields where they were developed.

In TRIZ, the forty principles and the contradiction matrix are the most accessible tools.^32,17 Contradictions occur when trying to improve one characteristic or parameter of a technical system causes another characteristic or parameter of the system to deteriorate. A compromise solution is usually sought. In TRIZ, however, truly innovative solutions are those that resolve contradictions. In this technique, a technical system can be featured by several of thirty-nine generic characteristics (Table 1), such as weight, size, brightness, speed, strength, etc. Two characteristics define a contradiction that can be solved by studying the principles (Table 2) suggested in the contradiction matrix.²⁸

Table 1: 39 Characteristics (Parameters) in the TRIZ Contradiction Matrix
C1: Weight of a mobile object	C21: Power
C2: Weight of a stationary object	C22: Loss of energy
C3: Length of a mobile object	C23: Loss of substance
C4: Length of a stationary object	C24: Loss of information
C5: Area of a mobile object	C25: Loss of time
C6: Area of a stationary object	C26: Amount of substance
C7: Volume of a mobile object	C27: Reliability
C8: Volume of a stationary object	C28: Accuracy of measurement
C9: Speed	C29: Accuracy of manufacturing
C10: Force	C30: Harmful factor acting on an object from outside
C11: Tension/pressure	C31: Harmful factor developed by an object
C12: Shape	C32: Manufacturability
C13: Stability of composition	C33: Convenience of use
C14: Strength	C34: Reparability
C15: Time of action of a moving object	C35: Adaptability
C16: Time of action of a stationary object	C36: Device complexity
C17: Temperature	C37: Difficulty of detecting and measuring
C18: Brightness	C38: Extent of automation
C19: Energy spent by a moving object	C39: Productivity
C20: Energy spent by a stationary object

Table 2: 40 Inventive Principles in the TRIZ Contradiction Matrix
P1: Divide an object into independent parts	P21: Skipping
P2: Removal/extraction	P22: Convert harm into benefit
P3: Local quality	P23: Feedback
P4: Asymmetry	P24: Intermediary
P5: Merging	P25: Self-service and self-organization
P6: Universality	P26: Copying
P7: Nested structures	P27: Inexpensive short-lived objects
P8: Anti-weight	P28: Mechanics substitution
P9: Preliminary anti-action	P29: Pneumatics and hydraulics
P10: Preliminary action	P30: Flexible shells and thin films
P11: Beforehand cushioning	P31: Porous materials and membranes
P12: Equipotentiality	P32: Color changes
P13: Reverse	P33: Homogeneity
P14: Spheroidality – curved	P34: Discarding and recovering
P15: Dynamism	P35: Parameters and properties changes
P16: Partial, satiated or excessive actions	P36: Phase transitions
P17: Another dimension	P37: Thermal expansion
P18: Mechanical vibration	P38: Strong oxidants
P19: Periodic action	P39: Inert atmosphere
P20: Continuity of useful action	P40: Composite materials

Multi-criteria Decision Making

Another focus in conceptual design is on the solution selection process. In order to prevent parameter conflicts during product innovation development, there can be a list of solutions. Multi-criteria decision aid (MCDA) provides tools and procedures to help the decision makers achieve the desired solution in the situation of ambiguous and uncertain product environments. Instead of yielding a single solution, MCDA establishes a kernel of preferred solutions. Solving multi-criteria problem does not search out the hidden truth, but helps decision makers master the complex data involved in the problem and advance to a solution.³³ MCDA can solve decision problems:

1. A scientific and systematic approach for decision-making is developed,
2. An effective approach to eliminate personal biases in the decision making process is invented and
3. A method to measure designers' or users' preferences toward each decision criterion and balance the conflicting criteria in order to generate the most cost-effective decision can be set up.

Multi-criteria Decision Aiding (MCDA) Models

All MCDA models exhibit certain constraints:

• Analytical hierarchy process and fuzzy models can only handle ordinal data.
• ELECTRE III can analyze different criteria without converting them into a single scale; however, it uses upward and downward distillations in which the discrimination thresholds for cut-off levels are subjectively assigned.
• The superiority and inferiority ranking (SIR) method can process both cardinal and ordinal data. It provides six different preference structures and also incorporates outranking rationales for dealing with "poor" true-criteria preference structures. It generalizes the superiority and inferiority scores via generalized criteria introduced in PROMETHEE methods and can provide more information to represent decision makers' preferences toward each decision criterion.^10,35

The Integrated Approach

When compared to other creative concept generation methods, like brainstorming, brainwriting 6-3-5, QFD, etc., TRIZ is better-suited to inventive engineering solutions.²⁰ As such, requirements specified in client statements will be formulated in terms of the thirty-nine engineering characteristics of TRIZ. In order to compare the relative importance of the objectives or the translated characteristics, weights are assigned as appropriate. The weights are also used in the SIR analysis of the alternatives (from in-house or competitors). For these purposes, a weighted objectives tree will be constructed from the client statement in which the leaves in TRIZ characteristics serve as criteria for alternative selection.

The importance of different objectives and sub-objectives of product design with weighted objectives can be ranked and compared to variants by visualizing their weight value profiles.²⁷ The assignment, calculation and comparison of relative weights to the objectives and sub-objectives can be constructed into a weighted objectives tree.¹⁴ An objectives tree is better-suited for quick concept clarification while substance-field analysis and ARIZ better for detailed design.¹⁹

As the SIR method can handle both ordinal and cardinal data, permits the use of different preference structures by the decision-makers and is able to measure the superiority and inferiority intensities of alternatives, it is used for multi-criteria alternative selection in the integrated method. The proposed conceptual design is shown in Figure 3.

Figure 3: Overview of  TRIZ-SIR-Enhanced  Conceptual Design

SIR – Generalized Criteria

A multi-criteria problem is first formulated by using a set of alternatives (A₁, A₂ ¡ … A_m) and criteria (g₁, g₂ ¡ … g_n) and letting g_j(A_i) be the criteria value or performance of the i^th alternative Ai with respect to the j^th criterion g_j. Decision-makers need to assign thresholds and weightings for each criterion and alternative, and assign levels of performance g_n(.) for each criterion. Then a (m by n) decision matrix, D, is formulated as follows:

The level of performance can be measured as indices, numerical constants or values in different units for different criteria. Decision makers can choose from any of the six different preference structures shown in Figure 4 and Table 3 according to their knowledge about the criteria.^10,11,31

Figure 4: SIR – Generalized Criteria

Table 3: Equations of Generalized Criteria

With the difference in criteria d = g(A)-g(A')e (-a,a) and the intensity of the preference P(A,A') = f(g(A) – g(A')) = f(d)e[0,1], the parameters p and q are respectively the preference and the indifference thresholds, while e is the Gaussian standard deviation. Types 1, 2 and 4 are discrete functions while Types 3, 5 and 6 are fuzzy, i.e., the latter functions deal with grey areas between strict preference and indifference among alternatives.

Intensities of Superiority and Inferiority

After all g_n(.) are determined, comparison among alternatives is made on a pairwise basis. Equations (1) and (2) give the intensities of superiority and inferiority of alternative A_i when compared to other alternatives. S_j(A_i) and I_j(A_i) are superiority and inferiority scores respectively, that provide more detailed information than the decision matrix, D, because the intensities of superiority and inferiority given by the generalized criteria are taken into account.²⁹

(1)

(2)

The scores constitute the superiority matrix or the S-matrix:

(3)

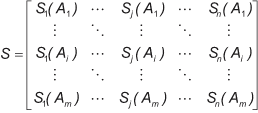
and the inferiority matrix or the I-matrix:

(4)

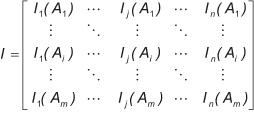
The two matrices include better information than the original decision matrix, D, because the intensity of superiority and inferiority given by the generalized criteria are taken into account. Also, the matrices convey different information because they represent different types of comparison results.

SIR-Simple Additive Weighting

The superiority and inferiority ranking (SIR) method (when using simple additive weighting (SAW) as the aggregation procedure) coincides with the second step of the PROMETHEE method.³⁵ The superiority and inferiority flows φ^>(.) and φ^<(.) are used to derive two complete rankings, R_^> = {P_>,I_>} and R_< = {P_<,I_<}, of the alternatives and the two complete rankings are then combined into a final partial ranking as the intersection of the two: R = {P,I,R} = R_>∩R_<.^11,30

 (5)

where

These two flows are used to determine AP_>A', AI_>A', AP

• The preference relation P by: APA' iff (AP_>A)' or (AP_>A' and AIA') or (AI_>A' and AP-A') (6)
• The indifference relation I by: AIA' iff AI_>A' and AIA' (7)
• The incomparability relation R by: ARA' iff (AP_>A' and A'P_<A) or (A'P_>A and AP_<A' (8)

Some synthesizing flows can be used to derive a complete ranking, such as the net flow in PROMETHEE,

φ_n(.) = φ^>(.)-φ^<(.)              (9)

and the relative distance in TOPSIS,

     (10)

The decision-maker uses the derived ranking (partial and/or complete) for further exploitation before a final decision is made. The MCDA process is summarized in Figure 5.

Figure 5: SIR Method Process

Case Study: Inline Skating Shoes

Inline skating is done on shoes that normally have four to five wheels arranged in a single line pattern. In general, the heel is used as a brake for stopping rather than using a toe stop. The mechanism of inline skating is similar on surfaces like skateboarding on roads or sidewalks. It may also work on special tracks and areas like skate parks and half-pipes. Some skaters compete in artistic skating events. The growth of inline skating was robust in the 1990s in the United States and then spread.

Due to their popularity, designers developed new casual sport shoes in combination with inline skating mechanism to become inline skating shoes. The real challenges for this type of trendy item are the appearance, functionality, convenience in use, etc. – a good example for using TRIZ with SIR to select the most competitive choice.

Assessment Criteria

There are hundreds of criteria in consideration when designing the shoe. Customers may select according to brand name (K2, Salomon, Rollerblade, UltraWheels). Marketing people may emphasize specific functions (K2 is proud of its soft boot, big wheels, long mount frames, aluminum-titanium alloy frame; Twincarn's ILQ-9 bearings, stability cuff, etc.).

But from NPD's point of view, more generic features should be adopted. In particular, the features chosen cannot block creative innovation. Upon market research, the design criteria of the product can be consolidated in terms of TRIZ characteristics (Table 1). Without loss of generality, the authors have identified eight TRIZ characteristics as the design criteria. According to the TRIZ concept of contradiction, these eight criteria determine the success of the product, but potentially contradict each other. Some criteria may reduce the side effect of some contradiction pairs, but may worsen the others. Another aid, therefore, the SIR method, is introduced to select the most appropriate alternative. The eight criteria in consideration are:

1. Stability of object C₁₃ – the retractable component. Can this component maintain a certain level of performance of the desired function even subject to strong forces such as the weight of the person? The higher the score, the more stable the candidate.
2. Strength C₁₄ – the structure of the parts (shoes and rollers). It must be strong enough to withstand being damaged from reasonable forces. The preferred alternatives should be more damage-resistant.
3. Durability of moving object C₃₀ – measuring the life of moving parts. The ability of moving objects to withstand frictional, collision damages accounts for their durability. Again, the higher score should be the more durable skate.
4. Reliability C₂₇ – compensational mechanisms/measures in the design of the product. What happens if the primary component, which is critical to the performance of the function or the safety of the user (e.g., presence of braking system), fails?
5. Manufacturability C₃₂ – compares the complexity of the process for manufacturing the product. This is not necessarily related to "complexity of system," because the latter can be measured according to the quantity of parts involved in the assembly of the product. The manufacturability can be poor in systems composed by a limited number of parts which have unique shapes or are to be made by special materials leading to manufacturing difficulties. A higher ranking means the high degree of manufacturability or difficulties; it is preferable to have a less complexity in the process.
6. Convenience of use C₃₃ – measures the time and procedures needed to complete each series of operations. The higher the score, the more convenient the use of the inline skates.
7. Complexity of system C₃₆ – roughly determined by counting the number of parts involved in the system. There is an overlapping area between "complexity of system" and "manufacturability," i.e., the required precision of the dimension of the parts, positions where each part is installed, need of calibration, etc. In a technical contradiction, a precise system may lead to another negative factor of complexity. In this case, a high score in complexity is less preferred than a lower score.
8. Bulkiness of component C₃₇ – most relevant to the product studied. As the retractability of the roller blade is one key component of the product, the way that individual design can make the retractable component minimal in size is the critical value of the design. This even relates to customer satisfaction. The lower the score, the more bulky the inline skates.

The above criteria are scored from 1 to 10 according to their performance precise to 2 decimal places; Table 4 shows the performance of three inline skating shoe examples based on these criteria.

Table 4: Performance of Inline Skates
	Models of Inline Skates
Selection Criteria	A1: KL-5001	A2: HG-3262	A3: FR-3019
g1: Stability of object	5.52	4.55	3.72
g2: Strength	3.74	6.23	4.82
g3: Durability of moving object	4.81	5.03	8.51
g4: Reliability	4.77	3.26	3.39
g5: Manufacturability	1	3	2
g6: Convenience of use	6.77	5.83	4.53
g7: Complexity of system	2.52	4.39	5.06
g8: Bulkiness of component	3.77	6.55	5.41

The SIR Process

After the candidates and the criteria for the ranking process are ready, the weight of each criterion is assigned. In order to match the desired functions, a weighted objectives tree is constructed such that the weight reflects the importance of individual criterion with respect to the total performance of the inline skates (Table 5).

Table 5: Features of Criteria Before Evaluation Process
Criterion gj	g1	g2	g3	g4	g5	g6	g7	g8
Type of Criterion	5	1	5	5	3	2	5	5
Weight Wj, SWj = 1	1/5	3/10	1/5	1/20	1/10	9/50	1/10	1/50
Preference Threshold, p	1.5	N/A	3	2	N/A	N/A	3	3
Indifference Threshold, q	0.5	N/A	0.1	1	N/A	1	0.1	1
Non-decreasing/non-increasing (1/0)	1	1	1	1	0	1	0	0

Figure 5: Weighted Objectives Tree of Inline Skates

Next, the criterion type and the threshold values are assigned accordingly. From Equations (1) to (4), the S-matrix and the I-matrix are calculated.

S = [ S₁(A₁) S₂(A₁) S₃(A₁) S₄(A₁) S₅(A₁) S₆(A₁) S₇(A₁) S₈(A₁)

S₁(A₂)  S₂(A₂) S₃(A₂) S₄(A₂) S₅(A₂) S₆(A₂) S₇(A₂) S₈(A₂)

S₁(A₃) S₂(A₃) S₃(A₃) S₄(A₃) S₅(A₃) S₆(A₃) S₇(A₃) S₈(A₃) ]

and

= [ 1.47 0 0 1.76 1.667 1 0 0

0.33 2 0.04 0 0 1 0.085 0

0 1 2 0 0.667 0 1.085 0.14 ]

I = [ I₁(A₁) I₂(A₁) I₃(A₁) I₄(A₁) I₅(A₁) I₆(A₁) I₇(A₁) I₈(A₁)

I₁(A₂) I₂(A₂) I₃(A₂) I₄(A₂) I₅(A₂) I₆(A₂) I₇(A₂) I₈(A₂)

I₁(A₃) I₂(A₃) I₃(A₃) I₄(A₃) I₅(A₃) I₆(A₃) I₇(A₃) I₈(A₃) ]

and

= [ 0 2 1.04 0 0 0 1.685 1.14

0.47 0 1 1 1.667 0 0.085 0

1.33 1 0 0.76 0.667 2 0 0 ]

The ranking process continues by using Equations (5), (9) and (10) to generate the S-flows, the I-flows, the n-flows and the r-flows (Table 6).

Table 6: Superiority and Inferiority Flows
S-flows	I-flows	n-flows	r-flows
φ>(A1) = 0.7287	φ<(A1) = 0.6993	φn(A1) = 0.0294	φr(A1) = 0.5101
φ>(A2) = 0.6425	φ<(A2) = 0.5192	φn(A2) = 0.1233	φr(A2) = 0.5531
φ>(A3) = 0.728	φ<(A3) = 1.1527	φn(A3) = -1.1527	φr(A3) = 0.4525

From Table 6's S-flows and I-flows and using Equations (6)-(8), the two complete rankings are:

R_>: A₁ → A₃ → A₂

R_<: A₂ → A₁ → A₃

The outranking relationships are (> means outrank, ~ means indifferent):

A₁>A₃   A₃~A₂

A₁~A₂

A partial ranking sequence is resulted by combining the two flows:

R = R_>∩R_<:  

In other words, superiority and inferiority flows together cannot tell whether A₁ or A₂ is preferred. From Table 6, the complete rankings by n-flows and r-flows are:

R_n: A₂ → A₁ → A₃

R_r: A₂ → A₁ → A₃

As a result, A₂ is the first choice as it ranks higher in net flow and has a larger relative distance value when compared to A₁. The overall ranking order is depicted in Table 7.

Table 7: Final Ranking of Inline Skates
1	A2: HG-3262
2	A1: KL-5001
3	A3: FR-3019

In addition, weights corresponding to the characteristics "Strength" (g₂) and "Bulkiness of component" (g₈) are greatest in Table 4. If g₂ is the improving factor and g₈ the worsening factor, the contradiction matrix suggests principles P₃₉, P₃, P₃₅ and P₂₃ be used for further investigation on alternative HG-3262.

Discussions

The 39 TRIZ characteristics in the classical contradiction matrix have not changed since the 1970s. Problems may arise when associating real-life engineering design functions with the 39 TRIZ characteristics. For the simple design problem in the example, the weighted objectives tree approach suffices.

Though it has been proposed to use SAW and TOPSIS to perform the aggregation process, these approaches will encounter the problem of variation in the final ranking, leading to inconsistent results; grey system theory may overcome the problem. One potential future direction is to incorporate the grey relational grade in formulating the superiority flows and the inferiority flows.^35,16 For example, S-flows become:

(11)

In Equation (11),

the grey relational grade can be applied to series with a minimum three points that facilitate applications with only a few criteria. and C^*_S1 and Cⁱ_Sj are indices of an augmented normalized decision matrix and re[0,1] is the distinguishing coefficient.

For the same test case, different student groups suggested different criteria, different weight objective trees, and different most preferred alternatives and contradiction pairs to be resolved. This is reasonable as there is no fair choice in decision making.⁷ As a result, no unique optimal design solution is achievable, particularly from a multi-disciplinary design team.

This paper only outlines the procedure in integrating concept clarification and multi-criteria alternative selection for the sake of innovative concept generation. The design and implementation of a full-fledged computer-aided conceptual design tool requires further research.

Conclusions

Innovative product development depends on unbiased systematic methods to generate innovative ideas. With the guidance of TRIZ, product designers are assisted with consolidating bundles of criteria into a reasonable range so that the core items of consideration on designing the product can be focused and the quality and competitiveness of the design can be maintained. From the case study, the three candidates have their own strengths and weaknesses. To determine which one is the most preferred, SIR can achieve its functions of evaluation of each alternative on individual criterion. The scoring and ranking approach makes the selection more scientific and logical. TRIZ and SIR fulfill their functions and complement to each other.

HG-3262 is ranked the top and can serve as a reference for the designer to develop the next successful inline skating shoe design.

Acknowledgement

The authors acknowledge the support offered by The Hong Kong Polytechnic University.

References

1. Akao, Yoji (1990). Quality Function Deployment: Integrating Customer Requirements Into Product Design. Productivity Press.
2. Al-Rashdan, D., Al-Kloub, B., Dean, A., and Al-Shemmeri, T., (1999) "Environmental Impact Assessment and Ranking the Environmental Projects in Jordan," European Journal of Operational Research, 118(1), pp.30-45.
3. Altshuller, G.S. (1984) Creativity as an Exact Science. Gordon and Breach Science Publishers.
4. Altshuller, G.S. (2002) 40 Principles: TRIZ Keys to Innovation. Technical Innovation Center.
5. Altshuller, G.S. (2000) The Innovation Algorithm: TRIZ, Systematic Innovation and Technical Creativity. Technical Innovation Center.
6. Arora, J.S. (1989) Introduction to Optimum Design. McGraw-Hill.
7. Arrow, K.J. (1951). Social Choice and Individual Values. Wiley.
8. Barda, O.H., Dupuis, J., and Lencioni, P. (1990), "Multi-criteria Location of Thermal Power Plants," European Journal of Operational Research, 45, pp.332-346.
9. Boothroyd, G. and Dewhurst, P. (1982) Computer-aided Design for Automatic or Manual Assembly. SME Technical Paper (Series) AD.
10. Brans, J.P. and Mareschal, B. (1990). "The PROMETHEE methods for MCDM; The PROMACALC, GAIA and BANKADVISER Software." In: Bana e Costa, C.A. (Ed.), Reading in Multiple Criteria Decision Aid. Springer, pp.216-252.
11. Brans, J.P., Vincke, Ph., and Mareschal, B., (1986). "How to Select and How to Rank Projects: The PROMETHEE Method," European Journal of Operational Research, 24, pp.228-238.
12. Carbone, F., De Montis, A., De Toro, P., and Stagl, S. (2000) "MCDA Methods Comparison: Environmental Policy Evaluation Applied to a Case Study in Italy," Proceedings of the 3rd Biennial Conference of the European Society for Ecological Economics (ESEE), Vienna University of Economics and Business Administration, Vienna, May 3-6, pp.1-23.
13. Cooper, R. G. (1993) Winning at New Products. Addison-Wesley.
14. Cross, N. (1989) Engineering Design Methods. Wiley.
15. De Bono, E. (1967) The Use of Lateral Thinking. Jonathan Cape.
16. Deng, J. (2002) Foundation of Grey Theory. Huazhung University of Science and Technology (Chinese).
17. Domb, E. (1997). "Contradictions: Air Bag Applications," The TRIZ Journal, July 1997.
18. Domb, E. (2000) "Managing Creativity for Project Success," Proceedings of the 7th Project Leadership Conference, June 2000.
19. Fey, V. and Rivin, E. (2005). Innovation on Demand. Cambridge University Press.
20. Higgins, J. M. (2006). 101 Creative Problem Solving Techniques. New Management Pub. Co.
21. Higgins, J. M. (1995). Innovate or Evaporate. New Management Pub. Co. Rev. ed.
22. Hollins, B. and Pugh, S. (1987) Successful Product Design. Butterworth.
23. Huang, G. Q. (1996). Design for X: Concurrent Engineering Imperatives. Chapman & Hall.
24. Karagiannidis, A. and Moussiopoulos, N., (1997), "Application of ELECTRE III for the Integrated Management of Municipal Solid Wastes in the Greater Athens Area," European Journal of Operational Research, 97(3), pp.439-449.
25. Mann, D., Dewulf, S., Zlotin, B., and Zusman, A. (2003) Matrix 2003: Updating the TRIZ Contradiction Matrix. CREAX Press.
26. Page, A. L. (1991). "New Product Development Practices Survey: Performance and Best Practices," PDMA's 15th Annual Conference, Oct 1991.
27. Pahl, G. and Beitz, W. (1984). Engineering Design: A Systematic Approach. Springer.
28. Pinto, J. (1997) "Contradiction Matrix," The TRIZ Journal, July 1997.
29. Rebai, A., (1993). "BBTOPSIS: A Bag Based Technique for Order Preference by Similarity to Ideal Solution," Fuzzy Sets and Systems 60(2), pp.143-162.
30. Roy, B., Slowinski, R., and Treichel, W. (1992) "Multicriteria Programming of Water Resources Supply Systems for Rural Areas," Water Resources Bulletin 28 (1), pp.13-31.
31. Tam, C.M., Tong, T.K.L., and Wong, Y.W. (2004) "Selection of Concrete Pump Using the Superiority and Inferiority Ranking Method," Journal of Construction Engineering and Management 130(6), pp.827-834.
32. Tate, K. and Domb, E. 1997. "TRIZ: Tools for Accelerating New Product Development," Proceedings of the 1997 PMI Symposium.
33. Vincke, P. 1992: Multiple Criteria Decision-aid. Wiley.
34. Wallas, G. (1926). The Art of Thought. Jonathan Cape.
35. Xu, X., (2001). "The SIR Method: A Superiority and Inferiority Ranking Method for Multiple Criteria Decision Making," European Journal of Operational Research, 131(3), pp.587-602.

About the Authors:

Dr. Kai-ming Yu received his B.Sc. in mechanical engineering from the University of Hong Kong in 1985. He obtained his Ph.D. from the University of Hong Kong, Department of Mechanical Engineering in 1991. He worked in the Research Centre and Mechanical Engineering Department of the Hong Kong University of Science & Technology until 1993. He is currently an Associate Professor in the Hong Kong Polytechnic University Industrial and Systems Engineering Department. His research interests include CAD/CAM, CAE, PDM, reverse engineering and rapid prototyping technologies. He is also a Senior Member of the Society of Manufacturing Engineers. Contact Kai Ming Yu at mfkmyu (at) polyu.edu.hk.

Mr. C.T. Lau is a research assistant in the Department of Industrial and Systems Engineering at The Hong Kong Polytechnic University, Hong Kong, China. Contact C.T. Lau at htony_lau (at) yahoo.com.

Dr. K.L. Tong is a senior research assistant in the Department of Industrial and Systems Engineering at The Hong Kong Polytechnic University, Hong Kong, China. Contact K.L. Tong at tklmas (at) yahoo.com.

Mr. W.K. Wong is a graduate of the Department of Industrial and Systems Engineering at The Hong Kong Polytechnic University, Hong Kong, China.