Модель роста параметров технических систем с учетом изменения надсистемных запросов
А. Привень, А. Кынин
1 Введение
Данная публикации продолжает цикл статей, посвященных математическому описанию кривых роста технических систем. В предыдущих публикациях [1, 2] описаны простейшие из известных моделей и охарактеризованы требования к ним. Сравнивая известные модели, мы пришли к выводу, что из них наиболее приемлемой является модель Кольрауша

где P – выходная переменная (растущий параметр), P0 и P¥ – начальное и конечное (предельное) значения выходной переменной, t- время, t0 – начальный момент развития системы, t и b – параметры уравнения.
К числу достоинств модели относятся простота подбора ее параметров t и b, а также асимметрия расчетной функции P(t). Недостатки модели заключаются в том, что с ее помощью проблематично предсказать предельное значение P¥ и принципиально невозможно описать ситуацию задержки развития [3], проявляющейся в более или менее длительной остановке роста параметра P, после чего рост возобновляется.
В настоящей работе предлагается новая модель, включающая, в том числе, влияние надсистемных характеристик на параметр P. В полном варианте [4, 5] модель способна описывать разнообразные варианты изменения параметров системы, включая задержки, остановки и конкурентную борьбу параллельно развивающихся систем. Описываемый ниже упрощенный вариант модели обладает меньшей общностью: он способен описывать только довольно простые случаи роста параметров. Однако, в отличие от известных моделей, охарактеризованных в [1, 2], он позволяет единым образом описывать кривые разной формы: симметричные и несимметричные, с пологим и резким стартовым отрезком, с внезапной остановкой в конце пути. Также описана процедура подбора параметров модели по начальной части кривой, что дает возможность количественно предсказывать рост ключевого параметра системы в предположении отсутствия задержек в ее развитии.
2 Модель структурной релаксации в аморфных веществах как прототип модели роста параметров технических систем
S-образные кривые используются в различных областях науки и техники для описания весьма разнообразных по своей природе зависимостей. Одной из этих областей является химическая термодинамика аморфных веществ. Особенностью этих веществ является то, что в температурном интервале, называемом «интервалом стеклования», их физические свойства начинают зависеть не только от природы вещества и температуры (что характерно для всех прочих индивидуальных веществ), но и от того, по какому температурно-временному режиму они обрабатываются. Другими словами, даже при выдержке вещества при постоянной температуре (и давлении) его физические свойства (такие, как плотность, теплосодержание, показатель преломления и др.) могут изменяться во времени. В то же время, каждой температуре (при постоянном давлении) соответствует некоторое предельное состояние, к которому приходит это вещество при достаточно длительной выдержке при этой температуре. В этом состоянии все физические свойства вещества остаются неизменными неограниченное время до тех пор, пока не изменится температура вещества.
Если предшествующий температурно-временной режим был достаточно простым, то движение к этому пределу происходит по одному из вариантов S-образной кривой; при более сложных температурно-временнЫх режимах, предшествующих выдержке при постоянной температуре, кривая движения к предельному состоянию может также быть достаточно сложной и, в частности, содержать экстремумы.
Указанные особенности сближают поведение аморфных веществ с поведением технических систем, ключевые параметры которых также могут изменяться во времени по разным траекториям, простейшим случаем которых является S-образная кривая.
Учитывая сходство кривых изменения параметров, мы попытались найти сходство и в самих системах. Чтобы это сходство было понятным, ниже мы опишем основные принципы, на которых строится модель, описывающая изменения свойств аморфных веществ при их термообработке в интервале стеклования.
Модель предполагает, что система (в данном случае – химическая) может находиться в двух принципиально разных видах состояний: равновесном и неравновесном.
Если система находится в равновесном состоянии, то при неизменных внешних параметрах (температура, давление, состав окружающей среды) она будет находиться в этом состоянии неограниченно долго. Каждому набору внешних параметров соответствует свое равновесное состояние, а каждому равновесному состоянию – своя внутренняя структура системы и своя комбинация физических свойств вещества. Условно говоря, в равновесном состоянии система идеально «подогнана» под требования надсистемы, в роли которой выступает в данном случае окружающая среда.
Изменение любого из внешних параметров приводит к тому, что все характеристики равновесного состояния изменяются. Изменяются и характеристики «равновесной» структуры системы – например, длины связей между атомами. В результате структура системы, которая в прежних условиях была равновесной, теперь становится неравновесной – к новым внешним условиям она уже не «подогнана». Это инициирует процесс «подгонки» структуры системы под новые требования (диктуемые новым набором вешних параметров) – именно такой процесс и называется структурной релаксацией. В ходе структурной релаксации система постепенно приближается к новому равновесному состоянию, а ее физические свойства – к новым равновесным значениям.
В случае, если внешние параметры изменяются вновь, в системе стартует новый релаксационный процесс. При этом, если прежний процесс еще не закончен, то, согласно модели, он продолжает идти параллельно с предыдущим. Модель исходит из того, что все релаксационные процессы, проходящие в системе, являются независимыми друг от друга (принцип суперпозиции), и их влияние на структуру и свойства системы суммируется.
Модель также постулирует, что одно и то же изменение внешних параметров может запускать сразу несколько (в пределе, бесконечное число) разных релаксационных процессов с разными характеристиками, главными из которых является «весовой коэффициент», учитывающий относительное влияние разных процессов на свойства системы, и «время релаксации», характеризующее скорость приближения к равновесному состоянию. Предполагается, что эти процессы могут протекать в разных микрообъемах системы, в которых структура и свойства не вполне совпадают друг с другом (такая микронеоднородность характерна для любых аморфных систем). «Весовые коэффициенты», относящиеся к одному и тому же релаксационному процессу, могут различаться для разных физических свойств: на одно свойство этот процесс может влиять сильнее, чем на другое.
В качестве движущей силы релаксационного процесса модель рассматривает разность значений так называемого «внутреннего параметра» системы в текущем и равновесном состояниях. Такой параметр существует для каждого релаксационного процесса, и через него же рассчитывается влияние этого процесса а конкретные свойства системы. Чем больше значение этой разности, тем сильнее проявляется стремление системы к равновесию, и тем с большей интенсивностью (при прочих равных условиях) протекает этот процесс.
В вышеописанных положениях легко просматриваются аналогии с техническими системами.
Так, в качестве внешних условий представляется логичным рассматривать надсистемные требования к системе, такие, как покупательские запросы и иные рыночные стимулы, административные барьеры и прочие внешние по отношению к системе факторов. Если не все, то, по крайней мере, часть из них могут быть описаны в параметрической форме. Также в качестве надсистемных факторов можно рассматривать конкурентное «давление» альтернативных систем, пытающихся, с одной стороны, затормозить рост рассматриваемой системы, но в то же время стимулирующее ее к дальнейшему росту с целью выживания на рынке и вытеснения конкурентов.
При этом, если ситуация на рынке стабильна, развитие системы может приостановиться, иногда на достаточно длительное время, - в результате имеем задержку развития, причина которой известна как “good enough” [3]. Такая задержка является аналогом достижения равновесного состояния в вышеописанных химических системах.
Сами альтернативные системы могут рассматриваться как аналоги тех микрообъемов аморфного вещества, в которых протекают параллельно запускаемые релаксационные процессы.
В качестве аналогов свойств вещества логично предположить параметры технической системы. При этом, как и в аморфных веществах, в технических системах разные параметры могут по-разному зависеть от общего состояния системы: в частности, одни параметры могут изменяться быстрее, чем другие (что известно в ТРИЗ как одно из проявлений закона неравномерности развития технических систем).
Наконец, логично предположить, что чем больше различие между текущими характеристиками системы и надсистемными требованиями к ней, тем интенсивнее будут вестись работы по ее усовершенствованию, и, в итоге, тем быстрее она будет изменять свои параметры, приближая их к надсистемным запросам.
Таким образом, в целом можно говорить о существенной содержательной аналогии между процессами в химических и технических системах.
Мы намеренно не приводим здесь математических соотношений, описывающих модель структурной релаксации в аморфных веществах, дабы не утомлять читателя сложными формулами. Желающие могут ознакомиться с ними по книге [6]; очень кратко они также представлены в вышеупомянутых наших публикациях [4, 5], в которых описан полный вариант предлагаемой модели. Перейдем сразу к упрощенному варианту предлагаемой модели, описывающему относительные случаи роста параметров технических систем.
3 Упрощенный вариант предлагаемой модели
3.1 Математическая модель
В упрощенном виде математическая модель записывается в виде дифференциального уравнения
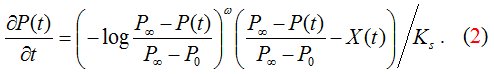
Величины Ks и w являются постоянными модели: предполагается, что их значения остаются неизменными в течение всего жизненного цикла системы.
Величина Ks характеризует общую динамику развития системы: чем она меньше, тем быстрее система доходит до предельного значения параметра Р. В грубом приближении, время, за которое значение параметра Р достаточно близко подходит к пределу (~0.9 P∞), составляет примерно 2...3 Ks.
Величина w, в нашем представлении, характеризует инвестиционную активность разработчиков: мы полагаем, что при равных значениях прибыли малые значения w соответствуют большим инвестициям в развитие системы, и наоборот. По нашему (впрочем ,пока еще не слишком большому) опыту, типичные значения w составляют от 0.7 до 1.3.
Переменная Х представляет собой «надсистемный» фактор. Эта переменная является функцией времени X(t), которая в простейшем варианте модели предполагается заранее заданной и независимой от самой системы.
Остальные обозначения расшифрованы выше.
Примем обозначение
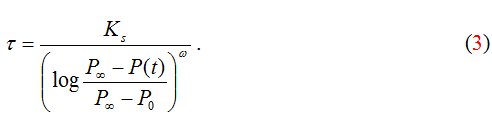
Величина t представляет собой время релаксации, характеризующее скорость отклика системы на внешнее возбуждение: после единичного мгновенного возбуждения изменение параметра Р за время, равное t, составляет » 63.2% от общей величины отклика системы (точное значение этой доли равно 1 – 1/е, где е – основание натуральных логарифмов). Поскольку величина t выражается через переменную Р, зависящую от времени, сама эта величина также является функцией времени.
С использованием времени релаксации уравнение (2) принимает вид
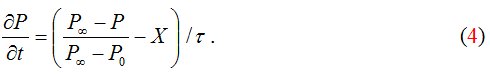
Модель можно дополнительно упростить, если использовать вместо переменных P, t и t «приведенные» значения этих переменных, выражаемые в виде
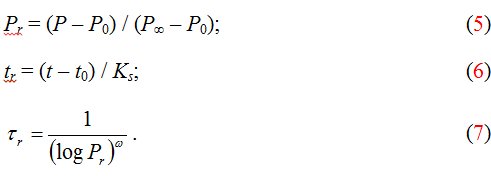
В приведенных переменных уравнение (2) принимает вид

Это уравнение легко решается численными методами (см. пояснения ниже). После нахождения решения в «приведенных» переменных оно может быть преобразовано к обычному виду с помощью формул

В уравнениях (8-10) значения X, tr, tr и Pr рассматриваются как функции времени.
Для того, чтобы по предлагаемой модели можно было производить практические расчеты, осталось определить, как зависит от времени «надсистемная» переменная Х. Практика показала, что для обычных «линий жизни», на которых нет задержек развития, достаточно ограничиться только двумя вариантами этой зависимости, которые являются простыми функциями приведенного времени tr:

На рис. 1 показаны кривые разной формы, рассчитанные с помощью предлагаемой модели. Как видно из рисунка, модель обладает достаточной гибкостью, чтобы при минимальном числе подгоночных параметров обеспечить разнообразие формы расчетных зависимостей P(t).
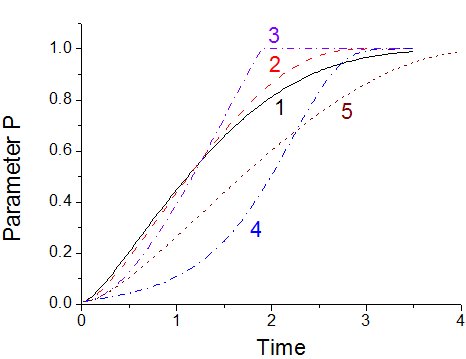
Рис.1. Результаты расчета по предлагаемой модели при значениях параметров:
1: X = t; w = 1; 2: X = t; w = 0.7; 3: X = t; w = 0.1; 4: X = exp(-3.7 + 2 t); w = 1; 5: X = t; w = 0.7. Во всех случаях принято P0 = 0, P∞ = 1. Для кривых 1-4 принято Ks = 1; для кривой 5, Ks = 1.5.
3.2 Алгоритм расчета и подбор постоянных модели
В дополнительном файле [7] описан алгоритм расчета по модели, приведен пример и приложен специальный файл, с помощью которого можно рассчитать кривую роста параметра Y при производных значениях постоянных модели P0, Pmax, t0, Ks и w.
Там же описана процедура подбора постоянных модели по начальной части «линии жизни», что позволяет предсказывать дальнейшее изменение параметра Р во времени в предположении отсутствия задержек развития системы. При этом предполагается, что значение t0 известно и, кроме того, известно несколько пар значений (t, P), соответствующих предыдущим (прежде всего, наиболее успешным) вариантам системы.
Значение Р0 также предполагается известным; во многих случаях, однако, можно производить расчеты, и не зная точно это значение, а просто принимая его равным нулю, что означает, что начальное значение параметра Р меньше, чем погрешность расчета по модели. Последнее допущение справедливо в тех многочисленных случаях, когда система в течение жизненного цикла многократно увеличивает значение своего ключевого параметра. К примеру, скорости современных автомобилей, самолетов или компьютерных вычислений совершенно несопоставимы с аналогичными характеристиками самых первых их моделей, и при прогнозировании будущих изменений этих характеристик (даже если бы такие прогнозы делались несколько десятилетий назад) начальными значениями этих характеристик вполне можно пренебречь.
Модель позволяет также подбирать предельное значение параметра Р¥, если оно заранее не известно. Такая возможность имеется в случае, если значение постоянной w не слишком мало (w > 0.6).
При малых значениях w < 0.3 расчетная кривая становится вырожденной: она быстро возрастает вплоть до достижения предела (Р»Р¥), после чего рост резко прерывается. Один из таких примеров будет рассмотрен ниже. В этом случае, не зная предела развития, с помощью модели можно предсказать только факт внезапного прекращения роста (поскольку значение w можно оценить и в этом случае), но нельзя предсказать, когда и при каком значении параметра Р это случится.
4 Примеры практического применения модели
Как указано в предыдущей публикации [8], форма «линий жизни» обычно наиболее близка к S-образной при выборе комплексных параметров, являющихся, в простейшем случае, произведением двух-трех ключевых параметров системы. Дополним: наилучшие результаты получаются в тех случаях, когда перемножаемые параметры находятся между собой в отношении технического противоречия, то есть увеличение одного из них, при прочих равных, ведет к уменьшению другого. Например, при равной цене монитора увеличение его диагонали сопровождается уменьшением разрешения, выражаемого числом пикселов на единицу линейного размера или площади монитора.
На рис. 2, 3 приведено два таких примера. В обоих случаях постоянные модели подбирались только по начальной (левой) части кривой, а остальная (правая) ее часть использовалась для проверки правильности предсказаний модели. Значения пределов развития определялись как подгоночные параметры (постоянные) модели. В обоих случаях часть кривой, используемая для определения значений постоянных модели, ограничивалась справа точками, соответствующими выходу системы на второй этап развития по традиционной периодизации [9, 10], как и указано в наших рекомендациях по подбору постоянных модели [7].
Как видим из рисунков, предсказания модели в целом неплохо согласуются с фактическими данными.
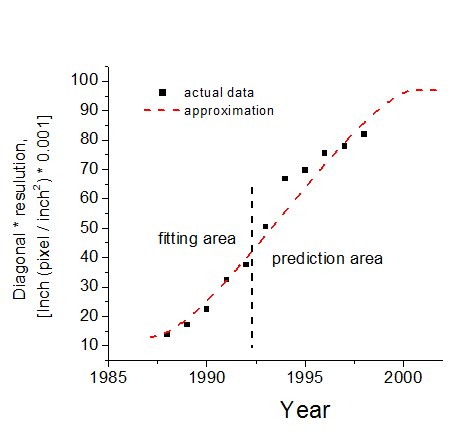
Рис. 2. Кривая роста ключевого параметра электронно-лучевых мониторов – произведения диагонали на разрешение.
Точки – данные [11], кривая – результат расчета по модели.
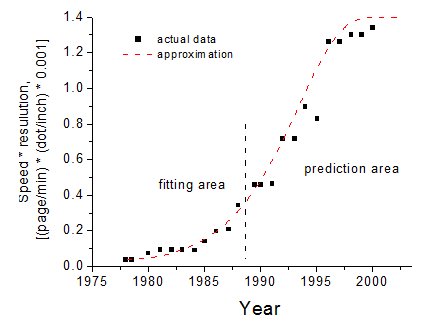
Рис. 3. Кривая роста ключевого параметра матричных принтеров – произведения скорости печати на разрешение.
Точки – данные [11], кривая – результат расчета по модели.
На рис. 4 показаны данные по росту прочности химических волокон из синтетических органических веществ. Этот пример отличается от предыдущих тем, что, во-первых, объектом совершенствования является не устройство, а материал, а, во-вторых, при определении постоянных модели не были использованы данные ни о верхнем пределе развития, ни о моменте возникновения системы. Последний был определен как подгоночный параметр и оказался равным 1885±3 года. И действительно, первое упоминание о реально произведенном, а не только задуманном, химическом волокне (искусственном шелке) относится как раз к 1885 году [12]. Процесс развития еще не закончен. Исходя из результатов моделирования, мы можем прогнозировать достижение химическими волокнами максимального значения удельной прочности около 250 МПа см3/г примерно к 2050 году.
Впрочем, появление искусственных волокон принципиально иной химической природы (например, сделанных из графена – особого вещества, атомная структура которого полностью лишена дефектов и в этом отношении подобна идеальному монокристаллу) может существенно увеличить это значение: ведь прогноз сделан, исходя из данных только об обычных искусственных волокнах. Аналогично, рассматривая только данные об автомобилях, едва ли можно было бы спрогнозировать рост скорости самолетов. Чтобы прогнозировать параметры систем, основанных на существенно разных разных принципах действия, необходимо, чтобы и исходные данные также относились к нескольким разным принципам действия, которые исторически сменяли друг друга.
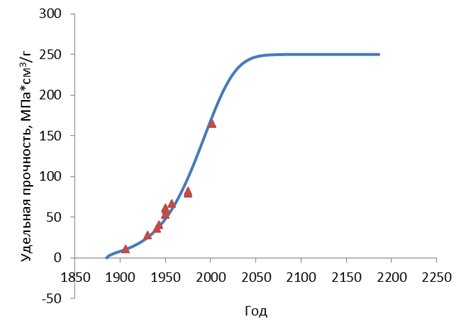
Рис. 4. Кривая роста удельной прочности (произведения прочности на удельный объем) химических волокон.
Точки – данные [13], кривая – результат расчета по модели.
Такой пример показан на рис. 5. В качестве комплексного параметра выбрано отношение производительности вычислений к их стоимости. Исходные данные включают все способы вычислений, начиная с ручного счета и заканчивая суперкомпьютерами. Авторы [14], собравшие эти данные, пришли к чрезвычайно интересному, на наш взгляд, выводу о том, что этот параметр в каждый момент времени был примерно одинаковым для всех реально конкурирующих систем. Мы полагаем, что это служит серьезным аргументом в пользу выбора именно такого показателя в качестве меры идеальности вычислительных систем. Однако в данном случае нас интересует возможность применения предлагаемой модели. Как видно из рисунка, модель вполне удовлетворительно описывает исходные данные (отдельные «провалы» на кривой и отдельные точки, расположенные существенно выше общей кривой, мы не учитываем). К сожалению, в данном случае неопределенность выбора как момента появления системы t0, так и начального и конечного значений параметра системы (с учетом того, что начальное значение в данном случае заведомо отличен от нуля) не дает возможности хотя бы приблизительно описать сценарий дальнейшего развития; нет возможности и оценить предел роста параметра. В данном случае мы сталкиваемся с ограничением применимости модели: в случае, если не известны ни момент появления системы, ни начальное значение ее параметра, то с помощью предлагаемой модели можно лишь аппроксимировать исторические данные, но не прогнозировать дальнейшее развитие системы. Если же эти параметры известны, то прогноз развития сделать можно.
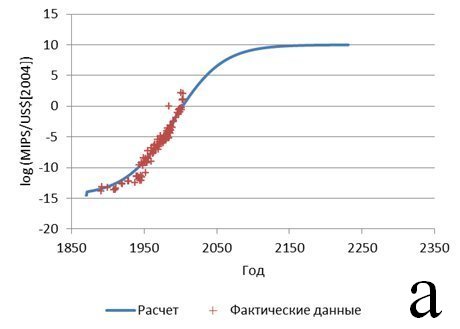
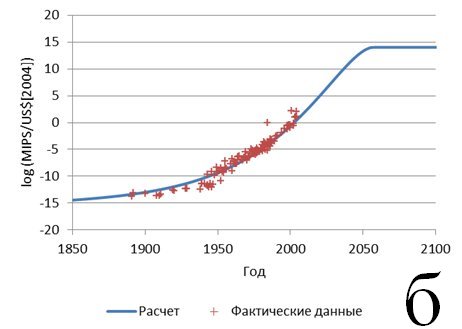
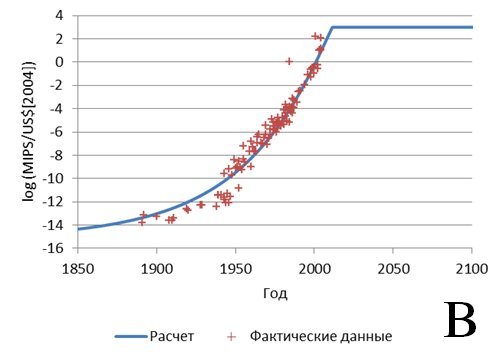
Рис. 5. Снижение стоимости вычислений (в качестве растущего параметра выбрано количество элементарных операций в секунду на единицу стоимости)
Точки – данные [14], линия – расчет при разных значениях t0 = 1880 (а), 1820 (б) и 1780 (в)
Существует, однако, еще одно ограничение применимости модели – это «вырожденный» случай с малыми значениями параметра w<0.45. В этом случае модель может предсказывать кривую роста параметра, но не может предсказать его предел – этот предел требуется определить заранее, исходя из физических или иных содержательных особенностей системы. Однако детальное рассмотрение этого вопроса требует отдельной публикации. Пример «вырожденной» кривой показан на рис. 5в.
5 О возможности описания «линий жизни» сложной формы
Все предыдущие примеры рассматривали кривые непрерывного роста ключевых параметров системы. Но, как известно (см. [3]), порой рост параметров системы приостанавливается или даже сменяется падением. Может ли предлагаемая модель учесть такого рода сценарии?
Данный вопрос разбивается на два:
- Способна ли модель описать такой сценарий хотя бы «задним числом»?
- Способна ли модель предсказать такой сценарий заранее, до того, как параметр прекратит свой рост или, тем более, начнет падать?
Ответ на первый вопрос с очевидностью положителен. В самом деле, варьируя «надсистемную» функцию X(t), можно получить любую кривую изменения параметра Р во времени, ограниченную только физическим пределом роста параметра Р∞. К примеру, если функция X(t) будет иметь форму синусоиды, то ту же самую форму (и ту же самую частоту) будет иметь и расчетная кривая изменения параметра Р.
Ответ на второй вопрос не столь прост. С одной стороны, как мы видели в предыдущем разделе, модель даже в предлагаемом очень упрощенном варианте способна предсказывать некоторые не вполне очевидные даже для специалистов особенности сценариев развития системы. С другой стороны, в этом упрощенном виде модель не может предсказать ни временную задержку развития (с последующим возобновлением роста параметров системы), ни, тем более, падение параметров. Таким образом, вопрос может стоять лишь о том, способна ли к таким предсказаниям более полная модель [4, 5]?
Ответ на последний вопрос может дать только практика. Из истории науки известно, что «объяснительные» модели, как правило, появляются раньше прогностических: далеко не всё из того, что наука может «объяснить», она способна спрогнозировать заранее.
Это же относится и к предлагаемой модели. Для того, чтобы понять, можно ли с ее помощью (пусть и в более сложном варианте) сделать правильный прогноз сложного сценария развития системы, необходимо, как минимум, научиться прогнозировать «надсистемную» функцию Х(t) в зависимости от сценария развития самой надсистемы. Это требует дальнейших разработок. Мы полагаем, что такие разработки достаточно перспективны. Приведут ли они к успеху – покажет только будущее.
6 Заключение
На основе аналогии с моделью, описывающей сложные кривые изменений физико-химических свойств аморфных веществ при их термообработке, предложена новая модель роста ключевых параметров технических систем. Из модели-прототипа заимствованы основные положения: о равновесном и неравновесном состояниях системы, о немгновенном (растянутом во времени) отклике системы на внешние воздействия (возмущения), называемом в физико-химии «релаксацией», о суперпозиции (наложении) параллельно протекающих в системе релаксационных процессов, и др.
В результате максимального упрощения модели построено достаточно простое математическое описание, позволяющее в рамках единого подхода и с использованием единого математического аппарата, путем изменения численных значений всего 2-3 постоянных, описывать кривые разнообразной формы, наблюдаемые на «линиях жизни» технических систем – зависимостях значений их ключевых параметров от времени.
Предложена процедура, позволяющая определить постоянные модели по начальному участку развития системы и, тем самым, предсказать дальнейший рост параметров в предположении отсутствия задержек развития системы, при условии, что она уже вышла на второй этап развития по традиционной для ТРИЗ периодизации развития технических систем. Результаты предсказаний по модели удовлетворительно согласуются с имеющимися в нашем распоряжении фактическими данными.
Модель, в числе прочего, позволяет предсказать предельное значение ключевого параметра системы. Такие предсказания возможны в случае, если кривая роста параметра не является «вырожденной». Является она таковой или нет, можно определить по значению одной из постоянных модели (w), подбираемой по фактическим данным о развитии системы. Если подобранное значение w составляет менее 0.45, то предельное значение растущего параметра необходимо определять из независимых данных.
Мы надеемся, что дальнейшие разработки позволят усовершенствовать модель и расширить область ее применимости, в том числе, и на сценарии с задержками развития систем. Оправдается наша надежда или нет, покажет будущее.
7 Список литературы
- Кынин А.Т. Модель развития технических систем, http://www.metodolog.ru/node/740
- Кынин А.Т., Привень А.И. Простейшие модели равития технических систем, http://www.metodolog.ru/node/940
- Кынин А.Т., Привень А.И. Задержки и остановки в развитии технических систем, http://www.metodolog.ru/node/910
- Priven A.I., Kynin A.T. Simple phenomenological model of “S-curve” growth in engineering systems. – In: Proc. 2nd Int. Conf. on Systematic Innovation (ICSI) & AITRI Innovation Week, Shanghai, 2011.
- Priven A.I., Kynin A.T. Simulation of changes of parameters of engineering systems during their development. – сб. трудов научной конференции ТРИЗ-ФЕСТ 2011.
- Мазурин О.В. Стеклование. Ленинград: Химия, 1986. 156 с.
- Процедура аппроксимации S-кривых с помощью модели Привеня – Кынина, http://files.mail.ru/AT3QDN
- Кынин А., Леняшин В., Фейгенсон Н. Выбор параметров для описания развития технических систем вдоль «линии жизни» // TRIZ-Fest 2009, 27-30 July, Saint Petersburg, Russia http://www.metodolog.ru/01697/01697.html
- Альтшуллер Г.С., Злотин Б.Л., Зусман А.В., Филатов В.И. Поиск новых идей: от озарения к технологии. (Теория и практика решения изобретательских задач). Кишинев: Картя Молдовеняске, 1989, http://www.trizminsk.org/r/4117.htm
- Любомирский А., Литвин С. Законы развития технических систем, 2003, http://www.metodolog.ru/00767/00767.html
- Sood A., Tellis G.J. Understanding the seeds of growth: Technological evolution and product innovation, http://www.marshall.usc.edu/emplibrary/wp04-04.pdf (accessed in 2009).
- A Short History of Manufactured Fibers, http://www.afma.org/f-tutor/history.htm
- Material performance trends // United Nations University, http://archive.unu.edu/unupress/unupbooks/uu24ee/uu24ee0a.htm
- Heebyung K., Magee Ch.L. A functional approach for studying technological progress: Application to information technology // Technological Forecasting & Social Change 73 (2006) 1061–1083.
Комментарии
Re: Модель роста параметров технических систем с учетом ...
А как насчет двери с несколькими замками - Вас, Фил, это никогда не смущало? Или Вы таких дверей никогда не видели? Посмотрите, например, здесь. Кстати, всё, что Вы видите на рисунках по ссылке, называется словом "дверь" - следует ли из этого, что все двери равны друг другу?
Re: Модель роста параметров технических систем с учетом ...
Re: Модель роста параметров технических систем с учетом ...
Вот именно - двери в чем-то равны. А уже ключи для этих дверей равны только в том, что они позволяют частично или полностью устранить препятствие к их открыванию.
Так и наши параметры: они "равны" в том, что их улучшение позволяет улучшить те потребительские свойства техники, за которые потребители частично или полностью отдают деньги, покупая эту технику. При этом точно так же, как для одной двери может существовать несколько замков и ключей, для данного вида техники может существовать несколько ключевых параметров. За улучшение каждого из них потребители будут платить. Впрочем, для Вас, Александр Владимирович, вряд ли нужно объяснять, что такое MPV :)
Не делаю тождества между MPV и теми параметрами, которые рассматриваются в статье, - опять же, просто указываю их общую черту: и тех, и других для данного вида техники может быть как один, так и несколько. И каждый из них - для чего-то ключевой. В нашем случае - каждый из таких комплексных параметров является "ключом" к техническому противоречию, выражаемому через входящие в него конкретные характеристики, такие, как разрешение принтера и скорость печати или удельный объем и прочность ткани.
Re: Модель роста параметров технических систем с учетом ...
Приветствую авторов!
Спасибо, хорошее наблюдение: комплексный параметр = произведение двух-трех ключевых параметров системы.
Точно ключевого?
Так, с слову: грамматическая ошибка в обозначении параметра по оси Y - resUlution. Д.б. resOlution.
Точно комплексного?
Точно ключевых?
Путаница с использованием терминов "ключевой" и "комплексный". Представляется, что правильно будет назвать обобщенный параметр комплексным, который включает 2-3 ключевых в виде произведения. Тогда везде будет единство: по ординате откладывается комплексный параметр, рассчитываемый, как Вами и предложено, в виде произведения двух-трех ключевых параметров системы. Вероятно, Ваше предложение окончательно отвечает на вопрос и закрывает тему "Что откладывать по оси Y" при построении кривой жизненного цикла.
И очень в тему замечание, что перемножаемые ключевые параметры находятся между собой в отношении технического противоречия, то есть увеличение одного из них, при прочих равных, ведет к уменьшению другого.
Еще раз спасибо за интересный и полезный материал.
Успехов,
AlexZ
P.S. Продолжение следует...
Re: Модель роста параметров технических систем с учетом ...
Спасибо Алексу за корректировку. В самом деле, "ключевым" лучше назвать, во избежание путаницы с "комплексным", именно отдельный параметр. Полностью принимаю формулировку "комплексный параметр = произведение двух-трех ключевых параметров, находящихся друг с другом в отношении технического противоречия".
Оговорки:
1. Бывает так, что в состоянии противоречия находятся параметры, у одного из которых значение фиксировано: хуже неприемлемо, а лучше не нужно. Один из примеров (упрощенно - есть нюансы, но не о них речь) - частотный диапазон аудиотехники, определяемый порогами человеческого восприятия. В этом случае второй параметр (например, динамический диапазон) может расти как бы "сам по себе". Существа дела это не меняет.
2. Слова "произведение" и "двух-трех" отражают наиболее простой вариант, но не единственно возможный. Разумеется, в каких-то случаях вид функции может быть и более сложным - например, параметры могут входить в выражение в степенях, отличных от единицы. Мы лишь утверждаем, что в тех случаях, с которыми мы столкнулись, этого варианта уже оказалось вполне достаточно для приближенного описания (а наша формула именно таковым и является).
3. В целом, в нашей формуле мы сделали довольно много упрощений для того, чтобы ее можно было достаточно просто применять на практике. Как говорил (если не ошибаюсь) Эйнштейн, "модель должна быть настолько простой, насколько это возможно, - но не проще". Именно этого мы и попытались достичь. Жизнь покажет, насколько хорошо это нам удалось...
Re: Модель роста параметров технических систем с учетом ...
Согласен с замечаниями Алекса по поводу комплексного и ключевых параметров.
Я бы ещё обратил внимание на важность выбора третьего параметра (как цена монитора в одном из примеров), при постоянном значении которого ключевые параметры находятся в противоречии (конфликте).
Этот параметр вроде точки подвеса рычажных весов, на чашках которых значения конфликтующих параметров.
И сразу же возникает вопрос:
"Этот параметр ("точка подвеса") всегда один и тот же на протяжении всего цикла, описываемого S-загогулиной, или их (параметров) может быть несколько?"
И второй вопрос:
"Один ли он (параметр) в каждой отдельной точке жизненного цикла, или их может быть несколько и в зависимости от выбора того или иного "меняется положение точки подвеса" а значит и форма кривой ?"
P.S. Переборщили с математикой:)
Re: Модель роста параметров технических систем с учетом ...
Спасибо. Это очень интересный разворот темы, над которым мы и сами думаем. Надеюсь, что-нибудь полезное и придумаем.
Пока что мы такой цели не ставили, а только лишь задались целью хотя бы как-то "оцифровать" S-кривую с учетом реального (а не воображаемого) разнообразия вариантов ее проявления. То есть - когда мы "зрительно" понимаем, что имеем дело именно с гладкой S-кривой (а не, скажем, с задержкой развития), то хотелось найти способ описать ее с помощью какого-то одного общего уравнения с минимальным числом подгоночных параметров (коэффициентов уравнения). В нашем случае таковых параметров образовалось "два с половиной" - "половиной" я называю здесь верхний предел, который иногда можно подобрать, а иногда нет (см. статью).
В отношении "точки подвеса" пока что могу сказать только то, что по крайней мере для каких-то случаев эту точку можно принять постоянной на всем жизненном цикле системы, и по крайней мере для каких-то других случаев - нельзя. Если сможем понять, как эти случаи различать, то, я надеюсь, мы сильно продвинемся в понимании существа как самой модели, так и закона повышения идеальности, на который, в идеале :), эта модель и должна нас вывести...
Отнюдь. Более простые варианты (из известных нам и реально работающих!) - это уравнение Кольрауша или уравнение логистической кривой. Мы их рассмотрели в предыдущей статье - см. ссылку 2. Сейчас сделали следующий шаг. Если Вы знаете, как дополнительно упростить эту модель (или построить иную модель, более простую, чем наша) без потери качества экстраполяции, будем очень признательны за информацию о таком варианте.
Re: Модель роста параметров технических систем с учетом ...
А Вы сформулируйте требования к параметру - "точке подвеса":)
Может окажется, что он таки один, но динамичный.
То, что его (системный) уровень выше, чем уровень ключевых параметров, требования к которым находятся в конфликте - по-моему ясно.
Таким образом S-загогулина превращаетсяся в граф приемлемых компромиссов, привязанных к графу изменения праметра - "точки подвеса".
Интересно что является таким параметром - "точкой подвеса" для живых организмов?:)
Этакий природный "товар, выделенный из общей массы товаров на роль всеобщего эквивалента" в конкретных условиях внешней среды.
P.S. Не смешите народ, говоря о "качестве экстраполяции"
Re: Модель роста параметров технических систем с учетом ...
Я так думаю, что отсюда будет прямой выход на сегментацию рынка (опять он, этот злосчастный рынок!): для каждой "точки подвеса" - свой сегмент. Причем эти точки, скорее всего, будут в общем случае изменяться в течение эволюционного цикла. Но вот насколько существенными будут эти изменения, и, в частности, в каких именно случаях они будут сопровождаться сменой ключевых параметров системы - я без фактических данных сказать не могу. Тех сведений, которыми я располагаю, для сколько-нибудь обоснованного ответа пока что мне не достаточно. Предположения на этот счет я могу сделать легко - но не хочу их обсуждать, пока не проверю их на каком-то числе примеров.
Про живые организмы - очень интересный вопрос и очень правильный, на мой взгляд. Но ответа у меня пока что тоже нет. Там тоже надо смотреть фактические сведения: например, по каким именно параметрам шел отбор в разные исторические периоды и по каким он идет на разных стадиях онтогенеза.
А вот про психологические корреляты как ключевых параметров, так и "точек подвеса" и изменений тех и других в течение жизненного цикла я подумаю обязательно - вполне вероятно, что в этой более-менее известной мне области и найдется в итоге приемлемое решение, как это не раз бывало раньше.
На эту тему мы можем подискутировать отдельно и подробно, поскольку всевозможными экстраполяциями эмпирических зависимостей я имел дело весьма часто и, в целом, не то чтобы безуспешно.
Часто озвучиваемую позицию "эмпирические зависимости экстраполировать нельзя в принципе" я отметаю сразу же - именно по той причине, что знаю по собственному опыту, что это не так, и, более того, понимаю, почему это не так и почему такое заблуждение существует. Конкретные детали, связанные с понятием "качество экстраполяции", готов обсуждать.
Re: Модель роста параметров технических систем с учетом ...
просто цитата
"Несмотря на то, что правдоподобных моделей одной и той же экосистемы можно предложить несколько (принцип множественности моделей Налимова), ни одной из них безоговорочно доверять нельзя (принцип контринтуитивного поведения Форрестера), как нельзя доверять и экспертам (принцип омнипотентности). В силу же четвертого принципа (несоответствия точности и сложности Заде) высокие стандарты точности при экологическом прогнозировании оказываются вообще недостижимыми."
П.М.Брусиловский
Re: Модель роста параметров технических систем с учетом ...
"... ни одной из них безоговорочно доверять нельзя...
... нельзя доверять и экспертам...
... высокие стандарты точности оказываются вообще недостижимыми..."
Из столь категоричных посылок следует, что нельзя доверять и П.М.Брусиловскому :)
Успехов,
AlexZ
Re: Модель роста параметров технических систем с учетом ...
Мне представляется, что эти принципы можно было бы сформулировать более лаконично, как это сделал один из героев "17 мгновений весны" (цитирую по памяти): "В этой жизни верить нельзя никому. Мне - можно."
Re: Модель роста параметров технических систем с учетом ...
Коллеги, приветствую!
IMHO: третий параметр является надсистемным по отношению к указанным двум противоречивым. Если воспользоваться примером с чашечными весами, то мы, двигая точку подвеса (значение 3-го параметра), можем уравновесить 2 "противоречивых" груза. Т.е. подсказать суть 3-го параметра поможет вопрос: "Во имя какого надсистемного параметра ТС мы разрешаем противоречие между двумя системными параметрами?" Или так: "Какой надсистемный параметр ТС улучшится, если будет разрешено противоречие между двумя системными параметрами?"
Трактовка "третий параметр является надсистемным по отношению к указанным двум противоречивым" может помочь ответить и про "точку подвеса" для живых организмов. Что происходит с живым организмом, когда ему удается разрешить противоречие?
Спасибо, коллеги! С Вами интересно...
Успехов,
AlexZ
Re: Модель роста параметров технических систем с учетом ...
В решении этого вопроса, IMHO, может помочь анализ размерностей конфликтующих друг с другом величин. Например, если при увеличении скорости движения (м/с) снижается пробег (м) и/или грузоподъемность (кг), то произведение этих величин (кг*м2/с) наводит на мысль о силе тяги, которая увеличивается при одновременном увеличении всех трех конфликтующих величин, - правда, в формулу для силы единицы входят в малость не тех степенях, поэтому, скорее всего, правильный ответ будет чуть иным. Не утверждаю, то этот прием является общим для всех случаев, но где-то помочь, я думаю, сможет.
Ну, то есть, как что? Расширяется ареал обитания, увеличивается численность популяции, появляются новые доступные ресурсы, а "в общем и целом" - как говорил классик - "жить стало лучше, жить стало веселее"... правда, появляются и новые проблемы.
Если попытаться предельно обобщить - то я полагаю, что при разрешении противоречия на каком-то уровне системной иерархии происходит переход от предыдущей фазы развития к последующей. Правда, я пока что не уверен, что на столь высоком уровне обобщения это может дать какой-то полезный результат. А на меньшем уровне обобщения, кроме приведенной цитаты, ничто на ум не приходит...
И Вам спасибо.
Re: Модель роста параметров технических систем с учетом ...
У меня возникла аналогия между "точками подвеса" и конструктами (репертуарные решётки)
http://www.metodolog.ru/node/965
А также с триадами Успенского, когда к двум взаимодействующим объектам (как веполь, например) добавляется третий "обеспечивающий взаимодействие" объект.
Например, в случае сидит человек на стуле (обекты: стул, человек и ... гравитационное поле) следует добавить третий объект Землю, как обеспечивающий взаимодействие.
То же самое касается и так называемой "образной сферы" - есть какой-то третий (и часто скрытый) "образ", который обеспечивает эмоциональную связь между образами.
Тут мы имеем "триаду" параметров - два находящиеся во взаимодействии (конфликте) и "обеспечивающий" параметр, который это взаимодействие обеспечивает.
Re: Модель роста параметров технических систем с учетом ...
Не смог остаться равнодушным, прочитав --
-- и вспомнив из того времени ещё более лаконичное: «Не доверяй никому. Даже себе самому. --И.Сталин».
Если без шуток, то хотелось все-таки уточнить вот что. Если после замечаний AlexZ вы принимаете формулировку "комплексный параметр = произведение двух-трех ключевых параметров, находящихся друг с другом в отношении технического противоречия", то расчетные графики на рис.5 могут быть совсем другие, так как на них первоначально представлены зависимости для отношения ключевых параметров.
Совпадут ли они после произведения с экспериментальными?
Если нет, то как все-таки рассчитывать компл.параметр – через произведение или отношение?
Re: Модель роста параметров технических систем с учетом ...
Присоединясь к вопросу VK - почему именно произведение? Как это можно было бы объяснить? Иными словами, каков физический смысл этого действия (почему не сложение или деление)?
Re: Модель роста параметров технических систем с учетом ...
Под термином "произведение" подразумевается алгебраическое умножение, в которое входит и деление (отношение).
А то, что не сложение... Умножение - это логическое И, означающее действие одного И другого фактора.
Уважаемые авторы, я правильно поясняю?
Успехов,
AlexZ
Re: Модель роста параметров технических систем с учетом ...
У меня тоже есть некие гипотезы по поводу и некие интерпретирующие образы, но мне интересно знать о том, как понятие раскрывают те, кто его использовал в данной работе. А деление означает (по моему) скорее введение еще одного параметра, обратного одному из исходных.
И что за физический смысл начинает при этом нести этот синтезированный комплексный параметр.
Re: Модель роста параметров технических систем с учетом ...
Несколько ответов на простой вопрос :)
1. Формальный ответ. Отношение А/В есть произведение А на величину, обратную В: А/В = А*(1/В). Следовательно, чтобы в данном случае (рис.5) остаться в строгих рамках данного определения, достаточно всего лишь взять в качестве второго ключевого параметра величину, обратную стоимости изделия. Произведение этой величины на число операций в секунду даст то самое, что отложено по оси У. Таким образом, с формальной точки зрения никаких противоречий сказанному на рисунке нет.
2. Содержательный ответ. В статье говорится, что мы берем произведение величин, находящихся друг с другом в отношении технического противоречия: увеличивая одно обычными (не изобретательскими) методами - уменьшаем другое. Если посмотреть на величины, изображенные на рис.5, то никакого технического противоречия между ними нет: увеличивая одну величину (неизобретательскими методами), мы одновременно увеличиваем и другую. Чтобы возникло отношение противоречия, мы одну из этих величин заменили на обратную ей. Далее см. п. 1.
3. Фактологический ответ. Согласившись с Алексом, я сделал несколько оговорок, в том числе и такую:
Беря для стоимости показатель степени, равный минцус единице, получаем обратную ей величину, которую мы и рассматриваем в качестве одного из ключевых параметров. Ее произведение число операций в секунду (второй ключевой параметр) дает то самое, что изображено на графике - см. п. 1, 2 выше.
4. Общефилософский ответ. Любая модель есть идеализация и упрощение, и любая модель применима при определенных условиях. К числу этих условий относятся в том числе и условия субъективные - например, умение пользователя модели анализировать исходные данные на предмет их соответствия формальным требованиям к этим самым данным. В случае нашей модели одно из таких требований - наличие технического противоречия между перемножаемыми параметрами. Если пользователь нашей модели не умеет определять, находятся ли перемножаемые параметры в отношении технического противоречия, то он не может использовать эту модель. Аналогично, если кто-то не имеет понятия о том, что такое квадратный корень, то он не сможет решить квадратное уравнение по известной формуле. Ведь, помимо самой формулы, для ее корректного использования иногда нужна еще и голова...
Re: Модель роста параметров технических систем с учетом ...
По поводу умножения и деления - см. выше. Мы в самом деле не подумали, что у кого-то могут возникнуть здесь вопросы. Уж слишком самоочевидным было для нас то, что, деля А на В, мы умножаем А на величину, обратную В. Увы - как это чкасто бывает - то, что самоочевидно для одного, не всегда самоочевидно для другого...
А вот следующие вопросы кажутся уже более интересными и содержательными.
1. Почему мы взяли именно произведение? Приведу цитату из Гаусса, отвечавшего на вопрос о том, почему в его знаменитой формуле используется именно такая функция, как квадрат. Он ответил, что можно использовать и другую функцию, а квадрат - всего лишь самая простая из всех возможных. В нашем случае, произведение - это тоже самая простая из всех возможных функций (еще более простая функция - сумма - не проходит в силу различия размерностей: складывать величины разных размерностей нельзя, а перемножать можно). Естественно, мы с произведения и начали, и, получив вполне удовлетворительный результат, не стали усложнять модель.
2. Каков физический смысл получившегося комплексного параметра? Думаю, какое-то приближение к ответу на этот вопрос может дать размерность получаемой величины. Например, произведение линейного разрешения принтера (размерность: пиксел/метр) на скорость печати (размерность: фактически метр/секунда) имеет в итоге размерность "пиксел/секунда", т.е. он фактичнеески характеризует число пикселов (различимых точек изображения), печатаемых принтером в единицу времени. В каких-то случаях интерпретация может оказаться более сложной.
Замечу в этой связи, что вопрос о физическом смысле эмпирических характеристик довольно активно обсуждается в научных кругах. Одна из распространенных точек зрений на этот счет заключается в том, что результат расчета по эмпирической формуле вообще лишен физического смысла. Я этой точки зрения не придерживаюсь и стараюсь использовать такие формулы, в которых не только результат расчета, но и составляющие самой формулы можно как-то осмысленно интерпретировать, т.е. приписать хотя бы приближенный физический смысл. По этой причине я почти никогда не использую полиномиальную регрессию: это как раз тот случай, когда коэффициенты уравнения действительно не несут никакого физического смысла, и, соответственно, результат расчета, скажем так, очень трудно осмысленно интерпретировать. Но это уже несколько другой вопрос, выходящий за рамки данной статьи. Готов подискутировать и на эту тему, если будет желание.
Re: Модель роста параметров технических систем с учетом ...
Примерно похожие вещи делал Фил, когда считал свои формулы активности. Там тормозило дело то, что каждый раз Филу приходилось на коленке придумывать новую формулу, в которую он включал то диаметр заборных отверстий турбин, то количество колес автомобиля и проч. То есть идея обобщенного параметра есть (и была до этого), а самого обобщенного параметра пока нет. Фил предлагает (упрощенно говоря) все параметры, которые можно отнести к активным, перемножать друг на друга, чтобы получить величину активности. А все, которые про защищенность - соединять в формуле защищенности. Там такая логика предлагается или просматривается. Непонятно как в общем случае отличить одно от другого, нет навыка конкретного счета и проч, но мысль такая.
А у вас какой подход к отбору того, что потом нужно будет перемножать?
Re: Модель роста параметров технических систем с учетом ...
Эт-не-серьезно :))
И всё-таки еще спрошу, если можно.
Мне хорошо знакома публикация, на которую в вашей статье эта ссылка:
-- и нужно сказать, что авторы говорят немножко о другом, прочитайте:
Если коротко пересказать по-русски, то говорится, что для одной функциональной категории, например, рассматриваемой вами скорости вычислений годовой прирост 1-го Функционального Показателя (ФП) вычислений в секунду (FPM calculation-per-second) и 2-го ФП вычислений-в-секунду-за-единицу-стоимости (FPM calculation-per-second per unit cost) примерно одинаковый. То есть речь идет совсем о другом, не о конкурирующих системах.
Надо сказать, что зависимость, которую вы используете на рис.5 имеет экспоненциальный характер кривой, которая в оригинальной статье приведена в логарифмическом масштабе и приближается к прямой. Почему у вас она коррелирует с S-кривой в лог.масштабе – не понятно...
Ещё небольшое недоразумение – по-моему, на рис.5 по оси ординат нужно исправить знак логарифма на десятичный :)
Просто замечу, что в той же статье [14], все приведенные данные развития технологических систем с высокой точностью аппроксимируются экспоненциальными зависимостями только. Показывается, что S-кривая развития технических систем и технологий – может рассматриваться, как частный случай, особенно при длительном периоде времени рассмотрения развития технологии. Потому что при длительном периоде набор S-кривых может успешно аппроксимироваться вновь экспонентой.
Хорошего настроения.
Re: Модель роста параметров технических систем с учетом ...
Разницу между нами и Филом в данном случае я вижу прежде всего в том, что Фил выдумал нечто из головы и не попытался, несмотря на мои многократные просьбы, сверить эту выдумку с фактами. Если бы сверил и у него получилось что-то реально интересное, то я бы вполне принял его подход. Но, увы, у меня нет никакой информации от Фила по поводу сопоставления его расчетов с какими-то фактическими численными данными. И это пока что единственная моя к нему претензия в этом отношении. (Теоретические построения Фила я принять не могу, но это совсем другой вопрос, к данной тематике прямого отношения не имеющий.)
Вообще, быть может (не уверен!), мы с Вами несколько разнимся в подходе к научному исследованию: Вы, как я понял (поправьте, если ошибся), требуете для формулы какого-то теоретического обоснования, тогда как для меня достаточно и эмпирического подтверждения. Формула, подтвержденная фактическими данными, для меня имеет статус "эмпирической формулы". Аналогичным путем был выведен, например, закон Кулона, который если и получил теоретическое обоснование (я не уверен), то только через несколько сотен лет после его эмпирического вывода.
Если кто-то хочет теоретически объяснить нашу формулу или, напротив, теоретически опровергнуть ее - мы (авторы) будем этому человеку очень признательны. Но сами этим заниматься пока что не планируем, ибо считаем на данный момент такой теоретический анализ преждевременным. Теориями мы займемся позже, когда будет достаточно эмпирического материала для их построения и фактической проверки. Пока же предоставляем это теоретизирование другим.
Re: Модель роста параметров технических систем с учетом ...
Обратите внимание на рис. 3 упомянутой статьи: на рис. (а) (один параметр) кривые, соответствующие разным принципам действия, ложатся каждая на свою кривую, а на рис. (b) (произведение нескольких параметров) - все на общую. Авторы пишут:
Но даже если бы они этих слов и не написали, то их рисунок весьма демонстративен: в каждый момент времени сосуществующие технологии давали близкие значения этого показателя, что и написано в нашей статье. Интерпретация авторов [14] нас в данном случае не интересовала - только факты.
По той простой причине, что слова "приближается к прямой" отражают субъективную позицию того, кто так говорит. Ему, видимо, показалось, что приближается, а нам вот так почему-то не показалось. Впрочем, Вы сами можете посмотреть на график (хоть в нашей статье, хоть в публикации [14] - графики построены по одним и тем же точкам) и решить, приближается зависимость к прямой или нет. Нас, однако, разнообразие мнений на этот счет мало интересует. Только факты.
А он и так десятичный :) - я привык к тому, что в технической литературе (в отличие, возможно, от математической - не знаю) "log" обозначает десятичный логарифм, а "ln" - натуральный.
"С высокой точностью" - это снова Ваше субъективное мнение. Можем сравнить точность описания общей зависимости, представленной на рисунке, экспонентой и нашей кривой - во втором случае среднеквадратичная ошибка получится в несколько раз меньше.
Разумеется, Вы вправе сказать, что никакой такой "общей зависимости" авторы этой публикации не привели и вообще никакого рисунка 3b не нарисовали. Но даже если бы они и не нарисовали, то данных, представленных в их таблицах, было бы уже достаточно для того, чтобы этот рисунок по этим данным нарисовали мы. Но мы не стали приписывать себе чужих заслуг и честно указали, что данная общая зависимость обнаружена не нами.
А что означает термин "успешно аппроксимироваться"? Снова Ваша субъективная оценка, которую невозможно оспорить по существу, ибо не указан критерий "успешности", а также сама успешно достигнутая цель (для чего аппроксимировать?). Если кому-то достаточно приблизить кривую прямой, не обращая внимание на кривизну, - они имеют на то полное право, и мы не смеем им в этом мешать. Нам для целей, указанных в статье, такой аппроксимации было не достаточно...
Хорошего настроения.[/quote]
Взаимно!
Re: Модель роста параметров технических систем с учетом ...
P.S. Экспоненциальные зависимости параметров системы от времени мы тоже видели и даже хотели привести в статье пару таких примеров, в качестве иллюстрации того интересного феномена, что экспонента, внезапно упирающаяся в какой-то момент в горизонталь, является одним из предельных случаев нашей модели. Но, к сожалению, сколько-нибудь детальное рассмотрение этого феномена потребовало бы еще, как минимум, 10-15 страниц занудного текста с формулами - мы посчитали такое добавление для данного сайта излишним. Похоже, мы правильно поступили: нам и так сделали замечание за "перебор" с математикой...
Re: Модель роста параметров технических систем с учетом ...
Уважаемые Фил и AlexZ,
Призываю вас перенести ваши разборки по поводу методики ФСА на отдельную ветку - пока что хотелось бы обсудить здесь разнообразные проблемы, связанные с количественным описанием кривых изменения параметров технических систем в процессе их развития.
Заранее благодарен за понимание.
С уважением,
Александр.
Re: Модель роста параметров технических систем с учетом ...
Уважаемый priven,
я мог бы отвечать вам по пунктам, но только коротко по-делу и без-обид, ладно ?
1.Вот вы пишите, например,
Привожу этот рис.(b) из [14] с нанесенными мною для ясности цветными кружками и линиями для отдельных информационных технологий:
Можно хорошо видеть, что значения упомянутого вами показателя по оси ординат для каждой из них не близки и разнятся в 10 раз и более.
Как вы считаете?
Re: Модель роста параметров технических систем с учетом ...
Спасибо, что избавили меня от необходимости нарушать копирайцт, приводя "закопирайченный" рисунок из статьи. Рекомендую все же через какое-то время удалить его из своего поста - так, на всякий случай. А этого вопроса по существу я ждал раньше, но Вы его никак не задавали, и вто задали, наконец. Отвечу.
А ответ заключается в том, что Вы снова привели субъективный аргумент, отражающий Вашу личную ьточку зрения, а именно - не указали критерий близости. А в этом ведь всё дело!
Вот есть, например, всемирно известная компания Schott, выпускающая оптические стекла. В каталоге этой компании есть разные стекла, ну, например, такие: стекло F2 с показателем преломления для линии d (587.562 нм), равным 1.62004, и стекло F5 с показателем преломления для той же линии, равным 1.60342. В обоих случаях ошибки не превышают 0.00001.
Можно ли считать, что показатели преломления этих стекол не близки? Конечно, можно! Ведь их разность (порядка 0.02) примерно в 2000 раз больше, чем ошибки измерения! Огромная величина для показателя преломления...
А можно ли считать, что показатели преломления этих стекол близки? Конечно можно! Ведь их разность примерно в 150 раз меньше, чем общий диапазон изменения показателя преломления в известных к настоящему времени стеклах (этот диапазон составляет примерно от 1.3 до 4.3). Эти два флинта - в сравнении со всеми вообще известными стеклами - обладают почти одинаковыми показателями преломления, и для целого ряда задач (например, для расчета радиационного теплообмена при высоких температурах - там тоже используется значение показателя преломления) различием между указанными величинами можно пренебречь без потери точности конечного результата (с учетом его ошибки).
Другими словами, конечный вывод о том, близки два значения или нет, зависит не только от самих этих значений, но и от решаемой задачи.
А теперь посмотрите еще раз на римсунок. Заодно посмотрите на рис. 3а из той же статьи, чтобы понять, что на рис. 3b, воспроизведенный Вами, попали отнюдь не все точки, а только небольшая часть из них - остальные точки оказались скрытыми.
Посмотрели? А теперь ответьте на вопросы:
(1) Являются ли точки, соответствующие разным технологиям, но одному моменту времени, очень далекими друг от друга по сравнению с общим диапазоном изменения величины (от 10 в -14 степени до 10 в +2 степени)? Размер - точнее, масштаб, - как говорится, имеет значение...
(2) Можно ли сказать, что разброс точек, относящихся к одному и тому же моменту времени и к разным технологиям, многократно больше, чем разброс между точками, относящимися к одному моменту времени и к одной технологии? Опять же, взгляните на рис. 3а - он даст Вам дополнительную информацию на этот счет.
Думаю, если Вы посмОтрите на рисунки непредвзятым взглядом и ответите на мои вопросы, то поймете, что у нас были достаточные основания утверждать о близости точек, которые Вам кажутся очень далекими.
А теперь перейдем собственно к задачам. В данном случае - к задачам прогнозирования роста параметров технических систем, которым, собственно, и посвящена статья. В данном конкретном случае - к задаче прогнозирования быстродействия компьютеров в исторической перспективе лет, скажем, на 30 или 50 (для иных целей строить подобный график в подобном масштабе я просто не вижу особого смысла). Быть может, я ошибаюсь, но думаю, что если кто-то сегодня спрогнозирует типичные значения этой самой характеристики на 2050-2060 годы с точностью до, скажем, двух порядков величины, то это будет величайшей силы прогноз. Наша модель - в данном конкретном случае - оказалась бессильной это сделать ввиду недостатка исходной информации для подбора значений параметров (не известен начальный момент времени t0 и не известен предел развития). Собственно, этот рисунок как раз и приведен нами для того, чтобы показать это ограничение области применимости нашей модели и предостеречь читателя от ее применения там, где сие мы считаем недопустимым.
Разумеется, Вы можете использовать те же самые данные для решения каких-то других задач, и в рамках Ваших задач вышеупомянутые точки будут очень далекими друг от друга. Но - это будут уже Ваши собственные выводы, касающиеся Ваших собственных задач. К нашей статье эти выводы отношения иметь уже не будут.
Если я недостаточно ответил на Ваш вопрос - готов продолжить дискуссию. Вопрос о субъективном и объективном в науке вообще и в математическом моделировании в частности меня интересует не только применительно к данной статье, но и сам по себе тоже, поэтому - с привязкой к предмету обсуждения - с удовольствием подискутирую еще.
С уважением,
Александр.
Только факты
Хорошо, priven, давайте тогда снова вернемся к вашей статье –
Теперь простой вопрос: покажите, где авторы [14] пришли к такому выводу или это вы считаете, что отношение производительности вычислений к их стоимости, например, для систем Early Computer (VaccumTube) и Personal Computer, представленных на рис.3b [14], является примерно одинаковым, хотя разница между ними около 100000 раз ?Пожалуйста, уважайте себя и других.
Re: Только факты
Прошу прощения, милейший, но... мы ведь говорили не про "весь интервал времени", а про "каждый момент времени". Разницу улавливаете? Вы в самом деле полагаете, что Early Computer (VaccumTube) и Personal Computer сосуществовали на рынке в один и тот же момент времени? Если да, то в какой именно момент времени это знаменательное событие имело место быть, и какими были в этот момент времени их показатели? Из упомянутой статьи вроде бы следует, что эти две технологиим во времени не пересекались... Единственное, что я готов здесь поправить, - это то, что речь в данном случае шла не о "конкурирующих" системах, а о "сосуществующих на рынке в одно и то же время системах, выполняющих одинаковую функцию и удовлетворяющих одинаковую потребность", - так будет точнее. Правда, обычно именно такие системы как раз и являются конкурирующими...
По поводу близости точек на графике я цитату из статьи уже привел. Мне достаточно того, что они сказали про "единый непрерывный путь описания кривой": из условий единства и непрерывности кривой, на мой взгляд, совершенно однозначно вытекает близость значений координат точек, относящихся к разным технологиям, на каждом участке этой самой кривой. Готов уточнить формулировку: авторы [14] обнаружили, что значения данного комплексного параметра, относящиеся к разному времени и разным технологиям, ложатся на единую непрерывную кривую, то есть в каждый момент времени значения этого параметра для сосуществующих технологий лежали в близких (существенно пересекающихся друг с другом) диапазонах - см. рис. 3b упомянутой статьи. Если Вас такая формулировка больше устраивает - пусть будет так.
Успехов!
Re: Только факты
1. Уже лучше!
И все же неинтеллигентно снова подкладывать авторам статьи то, что они не делали –
Меня же вполне устраивает как авторы [14] сами написали достаточно яcно об этом –
И подкладывать ничего не нужно.
2. Теперь о точности аппроксимации и субъективном мнении --
В статье [14, табл.3] авторы показывают (заметьте, не я), что все 6 приведенных экспоненциальных кривых имеют высокое значение показателя корреляции r2>0,9 с фактическими даными и узкий доверительный интервал +2,2 -- +4,9%%, особенно для данных после 1940г.
Как у ваших кривых с этим?
Re: Только факты
И у Вас тоже - но хотелось бы большего...
Вы не хотите видеть в статье слова про единую непрерывную линию (я привел цитату) - Ваши проблемы, далее этой темы касаться не буду. Поговорим о другом - о статистике.
Вы обратили внимание на то, что между функциональными категориями существуют статистически значимые различия. Не с чем спорить! Вопрос-то совсем в другом: с чем сравнивать? Я уже приводил пример двух стекол с ОЧЕНЬ сильно отличающимися показателями преломления - это если сравнивать с ошибкой измерения. И те же самые значения показателя преломления отличаются очень мало - если сравнивать с общим диапазоном изменения этого свойства.
Так и здесь: если сравнивать частные кривые друг с другом, то в их характеристиках можно найти статистически значимые различия. А если посмотреть на весь график в целом (что авторы статьи тоже сделали) - то можно говорить о единой линии, на которой эти самые кривые, несмотря на статистическую значимость различий между ними, можно рассматривать как части единой зависимости. Различимые - не значит далекие!
Повторю - весь вопрос в том, какую именно задачу мы решаем и какие свойства в связи с этим нас интересуют. Моя физическая сила очень мала по сравнению с Валуевым, она в сравнении с ним практически нулевая, если речь идет о нашем соревновании. Но наша сила примерно одинакова, если ее сравнивать с физической силой инфузории туфельки. Так примерно и здесь. Вы зациклились на одном аспекте, а мы рассматриваем совсем другой. И нам совершенно нет дела до того, являются ли различия между частными тенденциями статистически значимыми или нет. Мы нигде не говорим, что они полностью совпадают, а говорим, что они близки. Что именно Вас здесь не удовлетворяет?
У наших кривых с этим хорошо. Но приведенные Вами цифры, к сожалению, не с чем сравнивать. Коэффициент корреляции определен только для линейных зависимостей, каковой наша зависимость не является. Кроме того, авторы, насколько я понимаю, аппроксимировали другие завиимости. Поэтому давайте сравним то, что можно сравнивать.
Для нашей модели среднеквадратичное отклонение расчетных значений от экспериментальных составляет около 0.8 единицы десятичного логарифма, или примерно 5% от общего диапазона изменения величины, или примерно 20% от среднеквадратичного отклонения точек относительно среднего значения. Коэффициент корреляции между расчетными и фактическими значениями (только его я и могу здесь посчитать) составляет 0.98. Остаточная дисперсия составляет около 4% средней дисперсии исходнх данных.
При аппроксимации тех же данных экспонентой среднеквадратичное отклонение расчетных значений от экспериментальных составляет около 1.2 единицы десятичного логарифма, или примерно 8% от общего изменния величины, или примерно 30% от среднеквадратичного отклонения точек относительно среднего значения. Коэффициент корреляции составляет 0.95. Остаточная дисперсия составляет около 9% средней дисперсии исходнх данных.
В обоих случаях использованы все данные без изъятий.
На рисунке ниже Вы можете сравнить обе аппроксимации визуально.
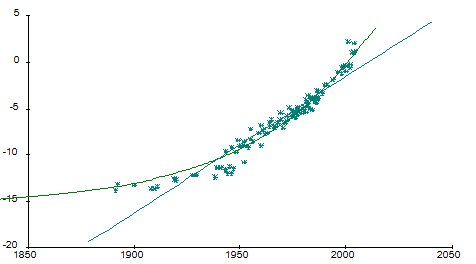
Результаты Вас устраивают?
Re: Только факты
-- и увы опять, не в той интерпретации которую подкладываете ей вы. Они ясно пишут о непрерывности тренда улучшения функционального параметра FPM «MIPSperUSD» и гдадкого его(тренда) соединения при смене очень разных информационных технологий друг другом. Прочитайте еще раз этот абзац. А вообще, уже надоело править вашу путаницу.
Priven, чес-слово.., вы привели цифры и фрагмент своей s-кривой, только там где она приближается к факт. данным, но не по краям её, где она грубо расходится с ними. Знаете, как это в науке зовётся ? :))
При этом предлагаемая авторами [14] экспонента соответствует фактическим данным во всем рассматриваемом диапазоне. И они справедливо утверждают (см.цитату выше), что на правом крае кривой для последних сорока лет факт.данные для технологии интегральных схем совпадают с общеизвестным экспоненциальным законом Мура.
Только без обид, но очевидно, что вы сознательно запутываете простые, в общем-то вопросы. Зачем, - не знаю, но соревноваться в этом с вами не хочется больше. Желаю вам разобраться с этим как-то, чтобы поверить сначала себе самому. А потом может и люди начнут...
Ну вот посудите сами, если название статьи звучит как «Модель роста параметров технических систем с учетом изменения надсистемных запросов», а через 10 страниц убористого текста в конце вдруг:
-- от такой «работы» ничего не остается, кроме стёба и лаконичного: «Не доверяй никому. Даже себе самому. --И.Сталин».
Re: Только факты
Да, для нас здесь важна именно непрерывность и гладкость единого тренда при смене технологий. Что означает в том числе и примерное совпадение значений параметра сосуществующих технологий в одинаковые моменты времени - ибо без этого не может быть непрерывности единой кривой. Путаницу я вижу пока что только в Вашей голове, в которой единая непрерывная кривая мирно уживается с разрывностью ее частей.
То, что Вы здесь написали, зовется словом "ложь". Данный фрагмент S-кривой проходит через ВСЕ точки, указанные в данной публикации, - как крайние, так и средние. Извинитесь хотя бы.
Что значит "соответствуют"? С какой именно точностью соответствуют? "Соответствие" - характеристика субъективная, если не указать количественный критерий, определяющий границу между "соответствием" и "несоответствием". Я, по Вашей просьбе, привел значения нескольких количественных статистических критериев, показывающих соответствие нашей модели фактическим данным. Заодно привел данные и для экспоненты, которая, правда, нас не интересует совершенно, но раз она Вас интересует - данные в Вашем распоряжении.
Вас такой разворот не устраивает? Не обессудьте - против Ваших убеждений мы возражать не станем, мы здесь обсуждаем только аргументы и факты.
Запутываете пока что Вы. Слова "очевидно, что сознательно", я могу понять только как проекцию Ваших собственных качеств на нас. Зачем Вам это надо - я не знаю.
Вопрос в самом деле очень простой - здесь Вы правы.
В некоей публикации есть фактические данные по росту некоторой характеристики со временем в широком временном интервале, включающем в том числе и несколько смен технологий. Эти данные, в пределах их разброса, ложатся на единую кривую, общую для всех технологий. Мы аппроксимировали эту кривую неким уравнением. Авторы упомянутой публикации тоже аппроксимировали эти данные, но по-другому и другим уравнением. Что именно Вас здесь смущает?
Одна и та же зависимость может быть аппроксимирована разными уравнениями. Выбор уравнения целиком является прерогативой того, кто проводит аппроксимацию. Они выбрали одно уравнение, мы выбрали другое. В чем вопрос-то?
Вопросы могут возникнуть только в том случае, если эти уравнения будут использоваться для решения какой-то конкретной задачи: одно из них может решить эту задачу лучше, другое - хуже.
В нашей статье рассматривается задача прогнозирования дальнейшего хода кривой (всей вместе), то есть - ее экстраполяция вправо. В статье [14] эта задача, вроде бы, не рассматривается. То есть вопрос о сравнении перед нами изначально вообще не стоял.
Вы попросили меня сравнить, с какой точностью два уравнения аппроксимируют исходные данные. Мы такую задачу перед собой не ставили. Но по Вашей просьбе я произвел необходимые выкладки и показал, что в этой части наша модель лучше. Замечу - если бы она оказалась хуже, то ровно ничего бы это для нас не изменило - опять же, по той причине, что мы не ставили перед собой задачу максимально точной аппроксимации исходных данных. Это совсем другая задача, которая почему-то заинтересовала Вас. Ну, заинтересовала - так заинтересовала. Я предоставил Вам объективные данные о точности аппроксимации одних и тех же данных двумя уравнениями - далее Вы можете делать из них любые выводы. Нас эта тема, повторяю, не интересует.
Напомню, что мы здесь обсуждали возможность предсказания кривых роста параметров при наличии задержек и остановок в развитии - и честно сказали, что пока что не можем этого сделать. Но суть Вашего вопроса я вижу в другом, а именно - в том, что Вы путаете учет некоего фактора с его предсказанием.
Приведу аналогию. Есть модель - закон Ома, с помощью которого мы можем предсказать силу тока в проводнике, зная его сопротивление и разность потенциалов на его концах. Но эта модель не может предсказать ту же силу тока, если разность потенциалов не известна. Разность потенциалов - это, по отношению к проводнику, надсистемная характеристика. Учитывается она в законе Ома? Да, безусловно, и если она известна, то можно делать предсказания. Но сам закон Ома не позволяет предсказывать значения этой характеристики - для этого требуется знание других фактов и других законов.
Точно так же и в нашем случае: наша модель позволяет учитывапть надсистемные факторы (о чем и сказано в заглавии), но (пока что?) не позволяет их предсказывать (о чем мы столь же честно пишем в заключении).
Если Вы полагаете, что после этого от нашей работы ничего не остается, - Ваше право так считать. Но это, опять же, Ваше субъективное мнение, которое сродни мнению о том, что закон Ома совершенно бесполезен, поскольку он не позволяет предсказывать разность потенциалов на концах проводника.
Разумеется, если бы наша модель могла предсказывать и задержки развития тоже, то она бы от этого сильно выиграла. Но, увы, мы не приписываем себе и нашим работам того, чего в них нет, и честно говорим, что вот это наша модель сделать может, а вот это - не может. А далее дело каждого решать, пользоваться этой моделью или нет. Собственно, это и есть, в моем представлении, научный подход.
Обид на Вас у нас нет (говорю от имени обоих соавторов). Есть слегка неприятное ощущение от того, что в Вашем лице мы видим квалифицированного эксперта, дающего почему-то замечания не по существу (что для Вас вообще-то не очень характерно) и зацикливающегося на деталях, не имеющих прямого отношения к предмету обсуждения. Но, поскольку в Вашей научной квалификации у нас сомнений нет, мы готовы пройти через и этот этап недопонимания, в надежде, что далее дискуссия все же пойдет по сути.
Re: Модель роста параметров технических систем с учетом ...
P.S. Возвращаясь к нашему с VK спору о единстве, непрерывности и примерном совпадении значений.
Представим ситуацию: в какой-то телепередаче женщина, отвечая на вопрос, есть ли у них с мужем дети, ответила: "Да, Маша, Таня и Света. Маша в этом году пошла в школу, Таня пойдет на следующий год а Света еще маленькая - она ходит в садик". И показали фотографию счастливого семейства. А я, ссылаясь на эти слова, сказал, что эта женщина рассказала о ее трех дочерях. При этом она сама не говорила, что у нее есть дочери, и не называла число "три" - это моя "придумка". Можно ли считать, что я таким образом исказил сказанную ею информацию?
Второй пример: в некоторой статье говорится о том, что детали А и В склеены друг с другом острыми концами, и нарисован чертеж их соединения. А мы говорим, ссылаясь на эту статью, что острые концы этих деталей имеют близкие значения пространственных координат. При этом авторы не употребляли слов "пространственные координаты" и , тем более, не говорили о близости оных, но эта близость вытекает как из рисунка, так и из слов о "склеивании". Можно ли сказать, что мы исказили высказывание авторов?
Третий пример. Некие авторы сказали, что величины А и В относятся друг к другу как 6:5. А мы, ссылаясь на эту публикацию, говорим о том, что величина А на 20% больше величины В. При этом авторы публикации не говорили о процентах и не называли число "20" - но оно математически вытекает из указанного ими соотношения. Исказили ли мы слова авторов?
Здесь, по-моему, совершенно аналогичная ситуация. Авторы [14] привели данные, построили по ним график зависимости некоторой величины от времени и указали, что в координатах, указанных на графике, эти данные, относящиеся к нескольким технологиям, образуют единую плавную кривую. Мы указали, что в статье показано примерное совпадение значений этой величины для сосуществующих технологий в одни и те же моменты времени.
Если эти ситуации чем-то отличаются друг от друга в плане "искажения данных" - то в чем именно состоят существенные различия?